Use short node IDs in your links (BB-7489)

I believe this changed when support for Git was added: the generated URLs that reference changesets use the full 40 character hexadecimal node ID.

I understand that it's nice to provide the full IDs: that way you don't need to implement logic to handle collisions any better than the underlying tools, i.e., you don't need to handle them on the assumption that SHA-1 is a secure hash function.

However,

• The long links are cumbersome: instead of a handy short node ID (12 characters for Mercurial) that will fit into most search boxes without clipping, I'm giving a 40 character string. That string is way to big for me to handle as anything but an opaque blob of bytes.

With a short node ID I can glance at it in an email and quickly see if it looks like it's the same as the one shown in my browsers address bar. I can copy a small node ID by hand in full — with a long ID I need to decide when to give up and when my prefix is long enough. I can paste a short ID into most tools without it overflowing the input field. Overall short IDs are more convenient and handy.

• The long links are almost always longer than what I'm comfortable pasting into text. The fixed text (https://bitbucket.org/.../.../commits/) take up 30 characters, so with 40 characters for the node ID we're already at 70 and then you need to add the username and repository.

The result is a 80+ character link which flows very badly in a text file or an email. I end up with lines longer than 80 characters which means that my diffs display badly in a standard width terminal.

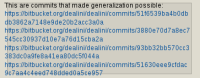
• The long links are mostly unnecessary. There are no collisions in the 275k changesets in the OpenOffice repository among the first 10 hexadecimal characters — there is a single collision among the first 9 characters.

This means that short links will work well in practice for almost all repositories.

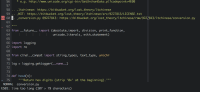
• You should actually handle collisions anyway: today I can shorten the Bitbucket URLs and they still work:

• • https://bitbucket.org/mirror/mercurial-crew/commits/9fbeb61b8ad2
  • https://bitbucket.org/mirror/mercurial-crew/commits/9fbeb61b8
  • https://bitbucket.org/mirror/mercurial-crew/commits/9fbeb6

However, I get a "404 Not Found" if the prefix becomes ambiguous:

• • https://bitbucket.org/mirror/mercurial-crew/commits/9fb

That ought to be handled better: present the user with a list of matching changesets