Chapter overview

This chapter is mainly about the abstraction of data, namely how to compound primitive data to make compound data. This type of abstraction will: - Elevate the conceptual level at which we can design our program - Increase the modularity of our design - Enhance the expressive power of our language.

Section 2.1 Introduction to Data Abstraction

Data abstraction is a methodology that enables us to isolate how a compound data object is used from the details of how it is constructed from more primitive data objects.

Basic idea of data abstraction is to structure the programs that are to use compound data objects so that they operate on abstract data. And in this abstraction, we hide the concrete data, and the interface between the two part is some procedures.

Section 2.1.1 Example: Arithmetic Operations for Rational Numbers

The author said that here we use the powerful strategy of synthesis: wishful thinking. Even we hanvn't get the concrete representation of rational number, we could get the procedure for doing arithmetic operation on rational number as follow:

#!scheme
(define (add-rat x y)
  (make-rat (+ (* (numer x) (denom y))
           (* (numer y) (denom x)))
        (* (denom x) (denom y))))

(define (sub-rat x y)
  (make-rat (- (* (numer x) (denom y))
           (* (numer y) (denom x)))
        (* (denom x) (denom y))))

(define (mul-rat x y)
  (make-rat (* (numer x) (numer y))
        (* (denom x) (denom y))))

(define (div-rat x y)
  (make-rat (* (numer x) (denom y))
        (* (denom x) (numer y))))

(define (equal-rat? x y)
  (= (* (numer x) (denom y))
     (* (denom x) (numer y))))

Then we can use different concrete data to represent the rational number, and if we offer the procedure numer, denom we will not change the upper level procedure such as add-rat, sub-rat etc.

Section 2.1.2 Abstraction Barriers

Abstraction barriers isolate different levels of the system. For example, functoin add-rat, sub-rat, mul-rat and div-rat will will not worry about how the rational number is represented, the only thing that they need to know is that the representation provided interface procedure such as numer and denom.

This simple idea has many advantages: - Make programs much easier to maintain and to modify - The concrete data can be represented in a variety of ways

Section 2.1.3 What is Meant by Data?

In generatl, we can think of data as defined by some collection of selectors and constructors, together with specified conditions that these procedures must fulfill in order to be a valid representation.

This point of view can used both in "hight-level" data object and "low-level" data object.

#!scheme
(define (my-cons x y)
  (define (dispatch m)
    (cond ((= m 0) x)
      ((= m 1) y)
      (else (error "Argument not 0 or 1: CONS" m))))
  dispatch)

(define (my-car z) (z 0))
(define (my-cdr z) (z 1))

(define tt (my-cons 2 3))

(my-car tt)
;Value: 2
(my-cdr tt)
;Value: 3

Such as the above example, we could build our own representation of cons cell.

Section 2.1.4 Extended Exercise: Interval Arithmetic

Section 2.2 Data and the Closure Property

Closure is the key to power in any means of combinations because it permits us to create hierarchical structure - structure made up of parts, which themselves are made up of parts, and so on.

In fact, closure is often regarded as one of the most powerful of scheme or common-lisp. The book Let over lambda use the whole chapter to explain how powerful closure and macro is.

Section 2.2.1 Representing Sequence

#!scheme
(cons 1 (cons 2 (cons 3 (cons 4 ()))))
; => (1 2 3 4)
(list 1 2 3 4)
; => (1 2 3 4)

Section 2.2.2 Hierarchical Structure

List can also used to represented hierarchical structure such as tree. In fact, we can notice that the recursive structure on list is only recursive on the cdr part of the list, but for hierarchical structure such as tree, it needs to recursion on both car and cdr part of the structure.

Scheme map function can not only used to list structure, but also can be used to tree like structure. When be used to tree like structure, one should recursive call the function on the

The following example shows that how to multiply a number to each node of a tree.

#!scheme
(define (scale-tree tree factor)
  (cond ((null? tree) '())
    ((not (pair? tree)) (* tree factor))
    (else (cons (scale-tree (car tree) factor)
            (scale-tree (cdr tree) factor)))))


(scale-tree (list 1 (list 2 (list 3 4) 5) (list 6 7)) 10)
;Value 16: (10 (20 (30 40) 50) (60 70))

This is a conventional scheme-like code, that recursive call on the car and cdr part of the tree, we could also use the following code to implement the same procedure.

#!scheme
(define (scale-tree tree factor)
  (map (lambda (sub-tree)
     (if (pair? sub-tree)
         (scale-tree sub-tree factor)
         (* sub-tree factor)))
       tree))

(scale-tree (list 1 (list 2 (list 3 4) 5) (list 6 7)) 10)
;Value 17: (10 (20 (30 40) 50) (60 70))

The above code use a map to recursively called on the part of the car part of the tree, so we will get the same result

Section 2.2.3

This section introduce conventional interface. The key idear of this is to use sequence operations to organizing programs so as to more clearly reflect the signal-flow structure. Since we could organize the data as list, so we can use the sequence operations to do the signal-flow program.

This section's filter was infact a build-in procedure of scheme, and accumulate is actually the build-in procedure reduce in scheme.

In functional programming, we seldom build program through change the state of variable, instead, we build program operat on list use procedure such as map, filter, reduce etc. For programmer from imperative language like C/C++, Java, it may take some time to adopt this philosophy.

In fact, new functional programmer always want to use loop such as in imperative programming, but in fact, it is a key step to get used to recursive and higher-order function to express loop. In this section, the book also show how to express nested loop use sequence paradigm. As the following example :

#!scheme
(define (enumerate-interval low high)
  (if (> low high)
      '()
      (cons low (enumerate-interval (+ low 1) high))))

(accumulate append
        '()
        (map (lambda (i)
           (map (lambda (j) (list i j))
            (enumerate-interval 1 (- i 1))))
         (enumerate-interval 1 4)))

;Value 29: ((2 1) (3 1) (3 2) (4 1) (4 2) (4 3))

This is like a nested loop in an imperative programming language as

#!C
for (int i = 1; i <= 4; ++i) {
    for (int j = 1; j < i; ++j) {
        // some code here
    }
}

So infact, we don't need explicit loop constructor to do nested loop in functional programming language, what we need, is to change our thinking mode from an imperative mode to functional mode.

Section 2.2.4 Example: A Picture Language

This section show the power of data abstraction and closure, also exploits explore higher-order procedures in an essential way.

This section presents a picture language, which also follow the framework start from the begining of the book that exphasized the importance of describing a language by focusing on the :

language primitives
its means of combination
its means of abstraction

The picture language also follow the same frame as scheme language, it only has one element called painter, and use operations such as beside to combine multiple painters. beside takes two painters and produces a new, compound painters that draw the first on the left, and the second on the right. Like a scheme cons operator. So we can use the operator to make complex painter structure like we did in scheme programming.

The picture language designed here show some critical ideas

abstraction with procedure and data
handle different basic drawing capabilities in a uniform way
combinating satisfy the closure property, permit us to easily build up complex designs.
stratified design : build complex in serveral level. The nth level only use primitive operation of the n - 1 th level's operation, not the operation before n - 1 th level.

All these will hep make programs robust. If we change the nth level primitives, we will only need to test the nth level and n + 1th level primitive operations. And will not affect other levels' operation.

Section 2.3 Symbolic Data

This section introduce the ability to work with arbitrary symbols as data.

Section 2.3.1 Quotation

In natrual language, we often use quotation marks to indicate that a word or a sentence is to be treated literally as a string of character. For example, if we ask "say your name aloud", we expect to hear answer such as "John", "Sussman" etc, but if we ask "say 'you name' aloud", we expect to hear exactly "your name".

In scheme programming, we follow the same practice. In fact, this practice break the general rule that all compound expression in scheme should delimited by parentheses, so there is a special form quote which is the same result as single quote, as the following example show:

#!scheme
(quote (a b c))
;Value 14: (a b c)
'(a b c)
;Value 15: (a b c)

(quote '(a b c))
;Value 16: (quote (a b c))

Section 2.3.2 Example: Symbolic Differentiation

This section use the program to perform symbolic differentiation of algebraic expressions. In fact, like the picture language in Section 2.2, this again is another small language develop to solve domain specific problem.

In fact, the following procedure is very similar like an interpretor of another language, evaluate expression according to different kind of expression:

#!scheme
(define (deriv exp var)
  (cond ((number? exp) 0)
    ((variable? exp) (if (same-variable? exp var) 1 0))
    ((sum? exp) (make-sum (deriv (addend exp) var)
                  (deriv (augend exp) var)))
    ((product? exp) (make-sum
             (make-product (multiplier exp)
                       (deriv (multiplicand exp) var))
             (make-product (deriv (multiplier exp) var)
                       (multiplicand exp))))
    (else (error "unknow expression type: DERIV" exp))))

Section 2.3.3 Example: Representing Sets

This section shows that set can be implement as unordered list, ordered list and binary tree. And different implementations have different efficiency on operations such as element-of-set?, adjoin-set etc.

From the example, we should learn in future how to choose an structure to represent some data-structure in an efficient way.

In designing a representation, one of the issues we should be concerned with is efficiency.

Simple analysis of the representation of ordered set will show that operation element-of-set? has time complexity O(n). Both intersect-set and union-set will require O(nm), n and m are respectively the size of two set.

One way to speed up the set operation in ordered list.

#!scheme
(define (element-of-set? x set)
  (cond ((null? false))
    ((= x (car set)) true)
    ((< x (car set)) false)
    (else (element-of-set? x (cdr set)))))

This is the element-of-set? using an ordered list representation. In the worst case, it will still use n step to judge, but on the best case, it will only cost 1 step and on average, it will require n/2 compare to find wether an element is in a set. Although the worst case is the same as a unordered set. On average, it will save us around half the time.

#!scheme
(define (intersection-set set1 set2)
  (if (or (null? set1) (null? set2))
      '()
      (let ((x1 (car set1)) (x2 (car set2)))
    (cond ((= x1 x2)
           (cons x1 (intersection-set (cdr set1) (cdr set2))))
          ((< x1 x2)
           (intersection-set (cdr set1) set2))
          ((< x2 x1)
           (intersection-set set1 (cdr set2)))))))

The procedure intersection-set under ordered list will take O(max(n, m)) time, n and m are the size of two set respectively. It is a considerable speedup over the unordered list implementation which will take O(mn).

The last representation of set is use a binary-search-tree to represent the set structure. In all the three representation, this one has the most efficient operation on almost all the operation.

The concrete structure of tree representation is as follow:

(define (entry tree) (car tree))
(define (left-branch tree) (cadr tree))
(define (right-branch tree) (caddr tree))
(define (make-tree entry left right)
  (list entry left right))

And use binary search tree, we can implement procedure element-of-set? in this way:

#!scheme
(define (element-of-set? x set)
  (cond ((null? set) false)
    ((= x (entry set)) true)
    ((< x (entry set))
     (element-of-set x (left-branch set)))
    ((> x (entry set))
     (element-of-set? x (right-branch set)))))

Section 2.3.4 Huffman Encoding Trees

This section use the knowledge of previous section to build a program for huffman encoding and decoding program.

Section 2.4 Multiple Representation for Abstract Data

In section 2.1.1, the author present data-abstraction barriers to seperated the layer of data representation. This is a powerful tools to for controlling complexity. By this, we can design a large program into smaller independent part.

But it is not so powerful. Sometimes, one data can be represented in more than one way, and we want our program can manipulate the two representation at the same time, such as complex number, which can be represent as real and imaginary part, but also can represented as magnitude and angle. This section use complex number example to show how how to cope with data that may be represented in different ways by different part of program, which is know as generic procedure.

The main idea behind generic procedure is to attach the data object with a type tag, which identify which representation it belongs to. And in the program we can cope with different type of object with different program. In fact, this technique is also the way to implement the dynmaic dispatch in OOP, and we can view the Class name is just a type tag of the Object.

Section 2.4.1 Representation for Complex Number

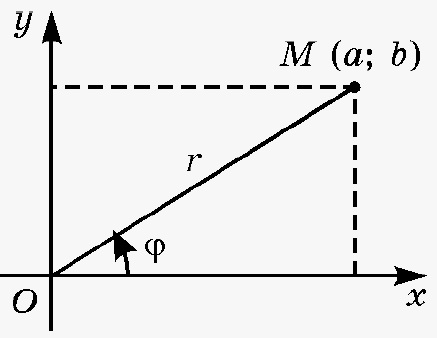
Complex Representation

As we can see from the above picture, complex can either represented as (a, b) or as (r, φ).

We can use data-abstraction barriers to seperated the concrete representation of complex number and the program to manipulate them. But we will have two seperated program to do with the two representation.

In the next section, we will see how to handle this problem.

Section 2.4.2 Tagged data

In fact, we could view the tagged data as a data with a type. An good introduction to type theroy is the Chapter 5 of the [Greg Michaelso][1]. In fact, this book also is a very well introduction book to lambda calculus.

In order to use tagged data type, we need procedure to attach tag to any data and extract the type and content of the data. Again, we use cons-cell to represent the tagged data.

#!scheme
(define (attach-tag type-tag contents)
  (cons type-tag contents))

(define (type-tag datum)
  (if (pair? datum)
      (car datum)
      (error "Bad tagged datum: TYPE-TAG" datum)))

(define (contents datum)
  (if (pair? datum)
      (cdr datum)
      (error "Bad tagged datum: CONTENT" datum)))

So use this technique, we could represent the complex data structure as follow:

#!scheme
;;;; manipulate for rectangle representation

(define (real-part-rectangle z) (car z))
(define (imag-part-rectangle z) (cdr z))
(define (magnitude-rectangle z)
  (sqrt (+ (square (real-part-rectangle z))
       (square (imag-part-rectangle z)))))
(define (angle-rectangle z)
  (atan (imag-part-rectangle z)
    (real-part-rectangle z)))

;;;; manipulate for polar representation

(define (magnitude-polar z) (car z))
(define (angle-polar z) (cdr z))
(define (real-part-polar z)
  (* (magnitude-polar z) (cos (angle-polar z))))
(define (imag-part-polar z)
  (* (magnitude-polar z) (sin (angle-polar z))))


;;;; tagged data part

(define (make-from-real-imag-rectangle x y)
  (attach-tag 'rectangle (cons x y)))

(define (make-from-mag-ang-polar x y)
  (attach-tag 'polar (cons x y)))

(define (rectangle? z) (eq? (type-tag z) 'rectangle))
(define (polar? z) (eq? (type-tag z) 'polar))

(define (real-part z)
  (cond ((rectangle? z) (real-part-rectangle (contents z)))
    ((polar? z) (real-part-polar (contents z)))
    (else (error "Unknow type: REAL-PART" z))))

(define (imag-part z)
  (cond ((rectangle? z) (imag-part-rectangle (contents z)))
    ((polar? z) (imag-part-polar (contents z)))
    (else (error "Unknow type: IMAG-PAET" z))))

(define (magnitude z)
  (cond ((rectangle? z) (magnitude-rectangle (contents z)))
    ((polar? z) (magnitude-polar (contents z)))
    (else (error "Unknow type: MAGNITUDE" z))))

(define (angle z)
  (cond ((rectangle? z) (angle-rectangle (contents z)))
    ((polar? z) (angle-polar (contents z)))
    (else (error "Unknow type: ANGLE" z))))

In fact, the above four functions are very similar. We could use an normal pattern function to abstract the four function.

#!scheme
(define (normal z f1 f2 error-string)
  (cond ((rectangle? z) (f1 (contents z)))
    ((polar? z) (f2 (contents z)))
    (else (error "Unknow type :" error-string z))))

(define (real-part z)
  (normal z real-part-rectangle real-part-polar "REAL-PART"))

(define (imag-part z)
  (normal z imag-part-rectangle imag-part-polar "IMAG-PAER"))

(define (angle z)
  (normal z angle-rectangle angle-polar "ANGLE"))

(define (magnitude z)
  (normal z magnitude-rectangle magnitude-polar "MAGNITUDE"))

Here again, we see the power of first-class function.

Section 2.4.3 Data-Directed Programming and Additivity

The previous section technique is dispatching on type. It is commonly used in Object-Oriented Programming language. But there are two weakness:

The generic interface procedures must know about all the difference representations.
Must ensure there is no name confliction

In this section, the author give ways to modularize the system design even further, which is called data-directed programming. It is often to make the procedure as a two dimentionaly table in Programming language, as following:

                                 Types
O                   Polar          |     Rectangle
p               -----------------------------------------
e  real-part    |real-part-polar   | real-part-rectangle
r  imag-part    |imag-part-polar   | imag-part-rectangle
a  magnitude    |magnitude-polar   | magnitude-rectangle
t  angle        |angle-polar       | angle-rectangle
i
o
n

In fact, if we are both familar with functional programming and OOP, we can notice, that OOP is often abstract on the Type dimention, while the functional programming generally abstract on the Operation dimention. The previous section's technique is actually a type of Object-oriented abstraction.

To implement data-directed programming, assume we have (put <op> <type> <item>) install the <item> in the table, and (get <op> <type>) looks up the <op>,<type> entry in the table and return the item found.

We could use an mutable hash-table in scheme to store the table as follow:

#!scheme
(define *op-table* (make-equal-hash-table))
(define (put op type proc)
  (hash-table/put! *op-table* (list op type) proc))
(define (get op type)
  (hash-table/get *op-table* (list op type) '()))

and then we could implementation the rectangular representation and polar representation as in the textbook.

#!scheme
;;;; representation of rectangular package
(define (install-rectangular-package)
  ;; internal procedures
  (define (real-part z) (car z))
  (define (imag-part z) (cdr z))
  (define (make-from-real-imag x y) (cons x y))
  (define (magnitude z)
    (sqrt (+ (square (real-part z))
         (square (imag-part z)))))
  (define (angle z)
    (atan (imag-part z) (real-part z)))
  (define (make-from-mag-ang r a)
    (cons (* r (cos a)) (* r (sin a))))
  ;; interface to the rest of the system
  (define (tag x) (attach-tag 'rectangle x))
  (begin
    (put 'real-part 'rectangular real-part)
    (put 'imag-part 'rectangular imag-part)
    (put 'magnitude 'rectangular magnitude)
    (put 'make-from-real-imag 'rectangular
     (lambda (x y) (tag (make-from-real-imag x y))))
    (put 'make-from-mag-ang 'rectangle
     (lambda (r a) (tag (make-from-mag-ang r a))))
    'done))

(install-rectangular-package)  ;;; install rectangular representation to system

The above is the representation of the rectangular form and the following is the representation of the polar form.

#!scheme
(define (install-polar-package)
  ;;internal procedure
  (define (magnitude z) (car z))
  (define (angle z) (cdr z))
  (define (make-from-mag-ang r a) (cons r a))
  (define (real-part z)
    (* (magnitude z) (cos (angle z))))
  (define (imag-part z)
    (* (magnitude z) (sin (angle z))))
  (define (make-from-real-imag x y)
    (cons (sqrt (+ (square x) (square y)))
      (atan y x)))
  ;; interface to the rest of the system
  (define (tag x) (attach-tag 'polar x))
  (begin
    (put 'real-part 'polar real-part)
    (put 'imag-part 'polar imag-part)
    (put 'magnitude 'polar magnitude)
    (put 'angle 'polar angle)
    (put 'make-from-real-imag 'polar
     (lambda (x y) (tag (make-from-real-imag x y))))
    (put 'make-from-mag-ang 'polar
     (lambda (r a) (tag (make-from-mag-ang r a))))
    'done))

(install-polar-package)    ;;; install the polar representation to system

And then we could implement the procedure apply-generic as follow:

#!scheme
(define (apply-generic op arg)
  (let ((type (type-tag arg)))
    (let ((proc (get op type)))
      (if proc
      (proc (contents arg))
      (error "No method for these types: APPLY-GENERIC:"
         (list op type))))))

(define (real-part z) (apply-generic 'real-part z))
(define (imag-part z) (apply-generic 'imag-part z))
(define (magnitude z) (apply-generic 'magnitude z))
(define (angle z) (apply-generic 'angle z))

(define c1 (cons 'rectangular (cons 1 2)))
(define c2 (cons 'polar (cons 4 0.718)))

(real-part c1)
;Value: 1
(real-part c2)
;Value: 3.012491975978806
(+ (real-part c1) (real-part c2))
;Value: 3.012491975978806

We could see that now we can apply procedure real-part to both rectangular form and polar form.

Message passing

Section 2.4.2 implement generic by dispatching on Types, which is the column of the table describe in section 2.4.3. And natually, we should wonder whether we could dispatch on row(operations).

#!scheme
(define (make-from-real-imag x y)
  (define (dispatch op)
    (cond ((eq? op 'real-part) x)
      ((eq? op 'imag-part y))
      ((eq? op 'magnitude)
       (sqrt (+ (square x) (square y))))
      ((eq? op 'angle (atan y x)))
      (else (error "Unknow op: MAKE-FROM-REAL-IMAG:" op))))
  dispatch)

(define (apply-generic op arg) (arg op))

This style of programming is called message passing. Message passing is not a mathematical trick but a useful technique for organizing system with generic operation.

Section 2.5 Systems with Generic Operations

Previous use generic technique to make operation work on different representation, namelly they are:

typed object
data-directed programming
message passing

This section will show how to use this idea not only on different representation but also work on different kinds of argument. This section show how to use data-directed programming to implement generic method on different type of argument.

Section 2.5.1 Generic Arithmetic Operations

This section shows in detail how to use data-directed programming to implement a arithemetic operations +,-,*,/ over number, rational, and complex numbers as showed in previous section.

The generic arithmetic procedures are defined as follows:

#!scheme
(define (add x y) (apply-generic 'add x y))
(define (sub x y) (apply-generic 'sub x y))
(define (mul x y) (apply-generic 'mul x y))
(define (div x y) (apply-generic 'div x y))

Then we could install different type package to handle the operations. The following is the ordinary number package:

#!scheme
(define (install-scheme-number-package)
  (define (tag x) (attach-tag 'scheme-number x))
  (begin
    (put 'add '(scheme-number scheme-number)
     (lambda (x y) (tag (+ x y))))
    (put 'sub '(scheme-number scheme-number)
     (lambda (x y) (tag (- x y))))
    (put 'mul '(scheme-number scheme-number)
     (lambda (x y) (tag (* x y))))
    (put 'div '(scheme-number scheme-number)
     (lambda (x y) (tag (/ x y))))
    (put 'make 'scheme-number (lambda (x) (tag x)))
    'done))

(install-scheme-number-package)

(define (make-scheme-number n)
  ((get 'make 'scheme-number) n))

(make-scheme-number 10)
;Value 13: (scheme-number . 10)

The rational package is like this:

#!scheme
(define (install-rational-package)
  ;;internal procedures
  (define (numer x) (car x))
  (define (denom x) (cdr x))
  (define (make-rat n d)
    (let ((g (gcd n d)))
      (cons (/ n g) (/ d g))))
  (define (add-rat x y)
    (make-rat (+ (* (numer x) (denom y))
         (* (numer y) (denom x)))
          (* (denom x) (denom y))))
  (define (sub-rat x y)
    (make-rat (- (* (numer x) (denom y))
         (* (numer y) (denom x)))
          (* (denom x) (denom y))))
  (define (mul-rat x y)
    (make-rat (* (numer x) (numer y))
          (* (denom x) (denom y))))
  (define (div-rat x y)
    (make-rat (* (numer x) (denom y))
          (* (denom x) (numer y))))
  ;;interface to the rest of the system
  (define (tag x) (attach-tag 'rational x))
  (begin
    (put 'add '(rational rational)
     (lambda (x y) (tag (add-rat x y))))
    (put 'sub '(rational rational)
     (lambda (x y) (tag (sub-rat x y))))
    (put 'mul '(rational rational)
     (lambda (x y) (tag (mul-rat x y))))
    (put 'div '(rational rational)
     (lambda (x y) (tag (div-rat x y))))
    (put 'make 'rational
     (lambda (n d) (tag (make-rat n d))))
    'done))

(install-rational-package)

(define (make-rational n d)
  ((get 'make 'rational) n d))

(make-rational 3 4)
;Value 14: (rational 3 . 4)

The complex number package is like follow:

#!scheme
(define (install-complex-package)
  ;;construct method
  (define (make-from-real-imag x y)
    ((get 'make-from-real-imag 'rectangular) x y))
  (define (make-from-mag-ang r a)
    ((get 'make-from-mag-ang 'polar) r a))
  (define (add-complex z1 z2)
    (make-from-real-imag (+ (real-part z1) (real-part z2))
             (+ (imag-part z1) (imag-part z2))))
  (define (sub-complex z1 z2)
    (make-from-real-imag (- (real-part z1) (real-part z2))
             (- (imag-part z1) (imag-part z2))))
  (define (mul-complex z1 z2)
    (make-from-mag-ang (* (magnitude z1) (magnitude z2))
               (+ (angle z1) (angle z2))))
  (define (div-complex z1 z2)
    (make-from-mag-ang (/ (magnitude z1) (magnitude z2))
               (- (angle z1) (angle z2))))
  ;;interface to the system
  (define (tag z) (attach-tag 'complex z))
  (begin
    (put 'add '(complex complex)
     (lambda (z1 z2) (tag (add-complex z1 z2))))
    (put 'sub '(complex complex)
     (lambda (z1 z2) (tag (sub-complex z1 z2))))
    (put 'mul '(complex complex)
     (lambda (z1 z2) (tag (mul-complex z1 z2))))
    (put 'div '(complex complex)
     (lambda (z1 z2) (tag (div-complex z1 z2))))
    (put 'make-from-real-imag 'complex
     (lambda (x y) (tag (make-from-real-imag x y))))
    (put 'make-from-mag-ang 'complex
     (lambda (r a) (tag (make-from-mag-ang r a))))
    'done))

(install-complex-package)

(define (make-complex-from-real-imag x y)
  ((get 'make-from-real-imag 'complex) x y))
(define (make-complex-from-mag-ang r a)
  ((get 'make-from-mag-ang 'complex) r a))

(make-complex-from-real-imag 3 4)
;Value 15: (complex rectangle 3 . 4)

Notice, that the complex number package used the rectangular and polar package of previous section.

Section 2.5.2 Combining Data of Different Types

The previous sections define procedure add, sub, mul and div for ordinary number, rational number and complex number seperately. And it is natually to ask whether we could do better: to define operations cross different type.

One way is to combine operations of different type and install them to our system. But this may be cumbersome. Since once we add a new type, we should not only install the new type operations, but also all the combinations of the operations with the new type and existing types.

Coercion

Another way is called coercion. Coercion is the process that view one type as another. Using this method, we can define type cast procedure and install them into a special coercion table.

#!scheme
(define (scheme-number->complex n)
  (make-complex-from-real-imag (contents n) 0)
  (put-coercion 'scheme-number
        'complex
        scheme-number->complex))

Procedure put-coercion and get-coercion manipulate the special coercion table. Then we can change the procedure apply-generic to adapt the coercion as follow:

#!scheme
(define (apply-generic op . args)
  (let ((type-tags (map type-tag args)))
    (let ((proc (get op type-tags)))
      (if proc
      (apply proc (map contents args))
      (if (= (length args) 2)
          (let ((type1 (car type-tags))
            (type2 (cadr type-tags))
            (a1 (car args))
            (a2 (cadr args)))
        (let ((t1->t2 (get-coercion type1 type2))
              (t2->t1 (get-coercion type2 type1)))
          (cond (t1->t2
             (apply-generic op (t1->t2 a1) a2))
            (t2->t1
             (apply-generic op a1 (t2->t1 a2)))
            (else (error "No method for these types"
                     (list op type-tags))))))
          (error "No method for these types"
             (list op type-tags)))))))

Hierarchies of types

The author suspect to tacle the problem of dealing with large numbers of interrelated types while still preserving modularity need to involve two things:

knowledge representation
automated reasoning

It may not be adequately addressed in terms of computer-language design alone.

Section 2.5.3 Example: Symbolic Algebra

This section use the simple but important part of algebraic manipulation to show how to apply the ideas of abstract data and generic operations to help organize the design of such system.

Arithmetic on polynomials

TODO in the future with whole 2.5 section

[1] http://www.amazon.com/Introduction-Functional-Programming-Calculus-Mathematics/dp/0486478831/ref=sr_1_fkmr1_1?ie=UTF8&qid=1366072379&sr=8-1-fkmr1&keywords=introduction+to+fp+through+lambda+calculus "An Introduction to Functional Programming through Lambda Calculus"

Wiki

SICP-solution / ch02-overview