Wiki
Clone wikiSICP-solution / ch03-overview
Chapter Overview
To organize large system, the previous knowledge of the book is not enouth. We must have some strategy to make the system into small modularities, each modularity contains coherent part that can be separately developed and maintained.
This chapter explore two prominent organizational strategies:
- Object
- Stream of information
Both these two approach raise significant linguistic issue in programming. With objects, we must be concerned with how a computational object can change and yet maintain its identity. This will force us to abandon our old substitution model and use a more mechanistic but less theoretically tractable environment model of computation. The stream approach can be most fully exploited when we decouple simulated time in our model from the order of the events that take place in the computer during evaluation. We will accomplish this using a technique know as delay evaluation.
Section 3.1 Assignment and Local State
Object approach:
- Decompos into computational objects and actual objects
- Computational objects model the actual objects in the system
- Each computational object must have its own local state variable describing the actual object's state
- The language must provide an assignment operator
Section 3.1.1 Local State Variable
#!scheme (define balance 100) (define (withdraw amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (withdraw 25) ;Value: 75 (withdraw 50) ;Value: 25 (withdraw 30) ;Value 14: "Insufficient funds"
(set! <name> <new-value>) change <name> so that its value is the result obtained by evaluating <new-value>.
But this implementation has some problem, balance was defined in global environment so it can be examined or modified by any procedure. A better way is to make balance internal to withdraw, we can do as follow:
#!scheme (define new-withdraw (let ((balance 100)) (lambda (amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")))) (new-withdraw 25) ;Value: 75 (new-withdraw 50) ;Value: 25 (new-withdraw 50) ;Value 15: "Insufficient funds"
In fact, this is a closure. And this is the pattern let-over-lambda. In fact, there is a book called this name.
A more elegant way to define such procedure is as follow:
#!scheme (define (make-withdraw balance) (lambda (amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds"))) (define W1 (make-withdraw 100)) (define W2 (make-withdraw 100)) (W1 50) ;Value: 50 (W2 70) ;Value: 30 (W2 40) ;Value 16: "Insufficient funds" (W1 40) ;Value: 10
Compare to procedure new-withdraw, the procedure make-withdraw do not use let to make balance a local variable, since formal parameters are already local.
We can even define a procedure that support not only withdraw but also deposit:
#!scheme (define (make-account balance) (define (withdraw amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (define (deposit amount) (begin (set! balance (+ balance amount)) balance)) (define (dispatch m) (cond ((eq? m 'withdraw) withdraw) ((eq? m 'deposit) deposit) (else (error "Unknow request: MAKE-ACCOUNT" m)))) dispatch) (define acc (make-account 100)) ((acc 'withdraw) 50) ;Value: 50 ((acc 'withdraw) 60) ;Value 17: "Insufficient funds" ((acc 'deposit) 40) ;Value: 90
Section 3.1.2 The Benefits of Introducing Assignment
Viewing systems as collections of objects with local state is a powerful technique for maintaining a modular design.
The author use monto-carlo pi estimate procedure to show how local state can make the program more clearly. In fact, the phenomenon illustrated by the Monto Carlo example shows that:
- One part of the program change over time
- Assignment help to hidden time-varying local state
- We can use assignment to reflect this behavior
Section 3.1.3 The Costs of Introducing Assignment
Everything is double edged(Is it true?). There must be some cost of introducing assignment. The costs are:
- Substitution model was not enough for our language
- No simple model with "nice" mathematical properties can be used to dealing with objects and assignment
Consider the following two program:
#!scheme (define (make-decrementer balance) (lambda (amount) (- balance amount))) (define D (make-decrementer 25)) (D 10) ;Value: 15 (D 20) ;Value: 5
#!scheme (define (make-simplified-withdraw balance) (lambda (amount) (set! balance (- balance amount)) balance)) (define W (make-simplified-withdraw 25)) (W 20) ;Value: 5 (W 10) ;Value: -5
The former one is without assignment, so it adapted to substutional model. The second one simulate a bank account, use assignment. In fact, the former one, give same input, it will guarantee to produce same output, but the second one, since the local state change, it will produce different output.
Programming without assignment is called functional programming.(This is a very unformal definition). Programming that make extensive use of assignemnt is called imperative programming.
Section 3.2 The Environment Model of Evaluation
Assignment make the substitution model no longer adequate. Now the variables must be considered some place to hold value. And will be maintained in a structure called environment.
Environment is a table of bindings.
Section 3.2.1 The Rules for Evaluation
To evaluatie a combination under environment model
- Evaluate the subexpressions of the combinations
- Apply the value of the operator subexpression to the values of the operand subexpressions
How to create a procedure under environment model
- A procedure is always a pair like (code, env)
- code is the λ-expression
- env is the environment in which the λ-expression is evaluated
How to apply a procedure under environment model
- Create a new environment containing a frame binding the parameters to the value of the arguments
- With the new environment, evaluate the procedure body
Section 3.3 Modeling with mutable data
This section showed data structure which has mutable state.
Section 3.3.1 Mutable List data structure
Mainly used function to operate on mutable list
(set-car! <arg> <value>): mutable set the car part of a cons cell(set-cdr! <arg> <value>): mutable set the cdr part of a cons cell
Sharing and identity
When we allow mutation, the effect of sharing elements between list and the identity of list is very important.
Mutation is just assignment
This section show that we can implement mutable data object using assignment and local state.
#!scheme (define (my-cons x y) (define (set-x! v) (set! x v)) (define (set-y! v) (set! y v)) (define (dispatch m) (cond ((eq? m 'my-car) x) ((eq? m 'my-cdr) y) ((eq? m 'my-set-car!) set-x!) ((eq? m 'my-set-cdr!) set-y!) (else (error "Undefined operation: CONS" m)))) dispatch) (define (my-car z) (z 'my-car)) (define (my-cdr z) (z 'my-cdr)) (define (my-set-car! z new-value) ((z 'my-set-car!) new-value) z) (define (my-set-cdr! z new-value) ((z 'my-set-cdr!) new-value) z)
Section 3.3.2 Represent Queue
Use mutation to represent an efficient queue data structure.
Section 3.3.3 Representing Tables
This section show how to use assignment to represent one-dimentional & two-dimentional tables(much like a hash-table in Python, Ruby).
The following is the code example for one-dimentional table
#!scheme (define (make-1d-table) (let ((local-table (list '*table*))) (define (lookup key) (let ((record (assoc key (cdr local-table)))) (if record (cdr record) #f))) (define (insert! key value) (let ((record (assoc key (cdr local-table)))) (if record (set-cdr! record value) (set-cdr! local-table (cons (cons key value) (cdr local-table)))) 'OK)) (define (dispatch m) (cond ((eq? m 'lookup) (lambda (v) (lookup v))) ((eq? m 'insert!) (lambda (k v) (insert! k v))) (else (error "1D-TABLE Unknow operation" m)))) dispatch)) (define t1 (make-1d-table)) ((nnt1 'lookup) 'a) ;Value: #f ((t1 'insert!) 'a 3) ;Value: ok ((t1 'insert!) 'b 4) ;Value: ok ((t1 'lookup) 'a) ;Value: 3
Here is the two-dimentional table:
#!scheme (define (make-2d-table) (let ((local-table (list '*table*))) (define (lookup key1 key2) (let ((subtable (assoc key1 (cdr local-table)))) (if subtable (let ((record (assoc key2 (cdr subtable)))) (if record (cdr record) #f)) #f))) (define (insert! key1 key2 value) (let ((subtable (assoc key1 (cdr local-table)))) (if subtable (let ((record (assoc key2 (cdr subtable)))) (if record (set-cdr! record value) (set-cdr! subtable (cons (cons key2 value) (cdr subtable))))) (set-cdr local-table (cons list key1 (cons key2 value) (cdr local-table)))) 'OK)) (define (dispatch m) (cond ((eq? m 'lookup-proc) lookup) ((eq? m 'insert-proc!) insert!) (else (error "Unknow operation on 2D-TABLE" m)))) dispatch)) (define operation-table (make-2d-table)) (define get (operation-table 'lookup-proc)) (define put (operation-table 'insert-proc!))
Notice, MIT-scheme has build in function make-1d-table and make-2d-table, see the MIT-scheme reference for detail.
Section 3.4 Concurrency: Time is of the Essence
The use of local state destroy the previous substitution model. The central issue is we admit time into our computational models.
Before we introduce time, our programs were timeless, in the sense that any expression that has a value always has the same value.
In physical world, Objects in the world do not change in sequence, in fact, they change concurrently.
It is often appropriate to divide computational models into parts that evolve separtely and concurrently. Even if the programs are to be executed on a sequential computer, the practice of writing programs as if they were to be executed concurrently forces the programs as if they were to be executed concurrently forces the programmer to avoid inessential timeing constraints and ths makes programs more modular.
We can also see that the introduce of assignment become even more problematic in the presence of concurrency.
Section 3.4.1 The nature of Time in Concurrent Systems
We may already know that when to concurrent processes handle shared memory, the result may be different. This is called race conditition, even worse is deadlock, in which case, the two processes wait for each other to release the shared resource and none of them can execute.
The root of this complexity lies in the assignments to variables that are shared among the different processes. We should be careful in writing programs use set!, because the result depends on the order of instruction. In concurrent case, we must be especially careful about assignments, because we can not control the order of the assignments made by the different processes.
One straight restriction on concurrency would stipulate that no operations that change any shared variables can occur at the same time. This would be both inefficient and overly conservative.
A less stringent restriction on concurrency would ensure that a concurrent system produces the same result as if the processes had run sequentially in some order. But this strategy may still have some problem, as the example in the textbook, Peter and Paul have a joint account start with $100, then Peter withdraw $40, concurrently Paul withdraw half of the money in the account, depend the sequential orders, the remain money may $30 or $10.
There are still weaker requirements for correct execution of concurrent programs. A program for simulating diffusion might consist of a large number of processes, each one representing a small volume of space, that update their values concurrently. Each process repeatedly changes it s value to the average of its own value and it neighbors' values. The algorithm converge to the right answer independent of the order in which the operations are done; there is no need for any restriction on concurrent use of the shared value.
Section 3.4.2 Mechanisms for Controlling Concurency
The root of difficulty in dealing with concurrent processes is rooted in the need to consider the interleaving of the order of events in the different process.
A practical approach to the design of concurrent systems is to devise general mechanisms that allow us to constrain the interleaving of concurrent processes so that we can be sure that the prgram behavior is correct. This section explore one of these approaches, called serializer.
Here is the example code using serializer. Notice the comment line, use a serializer to protected the operation withdraw and deposit.
#!scheme (define (make-account balance) (define (withdraw amount) (if (> balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (define (deposit amount) (set! balance (+ balance amount)) balance) (let ((protected (make-serializer))) ; serializer to protect (define (dispatch m) (cond ((eq? m 'withdraw) (protected withdraw)) ((eq? m 'deposit) (protected deposit)) ((eq? m 'balance) balance) (else (error "Unknow request: MAKE-ACCOUNT" m)))) dispatch))
Concurrent programming can be treacherously difficult when there are multiple shared resources.
The textbook give a example for exchanging two bank account as follow:
#!scheme (define (exchange account1 account2) (let ((difference (- (account1 'balance) (account2 'balance)))) ((account1 'withdraw) difference) ((account2 'deposit) difference)))
Suppose there are three accounts a1, a2 and a3, and Peter exchanges a1 and a2 while Paul concurrently exchanges a1 and a3. Even though the withdraw and deposit operations are protected by serializer, the exchange may produce incorrect result. Suppose that Peter compute the difference, and then Paul may already exchange the a1 and a3 account before Peter to complete the exchange. For the correct behavior, we must arrnage for the exchange procedure to lock out any other concurrent accesses to the account during the entire time of the exchange. The code looks like the following:
#!scheme (define (make-account balance) (define (withdraw amount) (if (> balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (define (deposit amount) (set! balance (+ balance amount)) balance) (let ((balance-serializer (make-serializer))) (define (dispatch m) (cond ((eq? m 'withdraw) (protected withdraw)) ((eq? m 'deposit) (protected deposit)) ((eq? m 'balance) balance) ((eq? m 'serializer) balance-serializer) ; return the protect serializer (else (error "Unknow request: MAKE-ACCOUNT" m)))) dispatch))
Notice that we dispatch the serializer to return the bank serializer. So that we can get the exchange code as follow:
#!scheme (define (deposit account amount) (let ((s (account 'serializer)) (d (account 'deposit))) ((s d) amount))) (define (serialized-exchange account1 account2) (let ((serializer1 (account1 'serializer)) (serializer2 (account2 'serializer))) ((serializer1 (serializer2 exchange)) account1 account2)))
Implementing serializers
Serializer can be implemented using a more primitive synchronization mechanism mutex, such as follow:
#!scheme (define (make-serializer) (let (mutex (make-mutex)) (lambda (p) (define (serialized-p . args) (mutex 'acquire) (let ((val (apply p args))) (mutex 'release) val)) serialized-p)))
Deadlock
TODO in the future.
Concurrency, time, and communication
The problems of concurrency lies deeper than the description of the above section. From a fundamental point of view, it's not always clear what is meant by "shared state".
So from my own point of view, wether the "shared state" is the right approach to solve the problem arised from concurrent programming and distributed programming is still unknow. So maybe the method like no-mutable data in programming language like Erlang is the right approach? It's only my own point of view.
Section 3.5 Stream
The previous section of this chapter handle the problem of assignment. The section 3.4 discuss the problem caused by using assignment when the program run concurrently.
This section, the author explore an alternative approach to modeling state, based on data structure called stream, and show that stream can mitigate some of the complexity of modeling state.
When introducing assignment, we view the world changing by the variable time. So we must use assignment to model the changes with time.
In type theory and functional programming, a stream is an infinite list, in mathematics, we can describe a time-varying behavior by a function x(t). If we concentrate on x instant by instant, we think of it as a changing quantity. Yet if we concentrate on the entire time history of valu, we do not emphasize change--the function itself does not change.
Stream processing lets us model systems that have state without ever using assignment or mutable data. This has important implications, both theoretical and practical, because we can build models that avoid the drawbacks inherent in introducing assignment. On the other hand, the stream framework raises difficulties of its own, and the question of which modeling technique leads to more modular and more easily maintained systems remains open.
Section 3.5.1 Streams Are Delayed Lists
map, filter and accumulate are elegant at the price of servere inefficientcy with respect to both the time and space required by our computations. When we represent manipulations on sequences as transformations of lists, our programs must construct and copy data structures(which may be huge) at every setp of a process.
#!scheme (define (sum-primes a b) (define (iter count accum) (cond ((> count b) accum) ((prime? count) (iter (+ count 1) (+ count accum))) (else (iter (+ count 1) accum)))) (iter a 0)) (define (sum-primes2 a b) (accumulate + 0 (filter prime? (enumerate-interval a b))))
Consider the above to procedure, the first one only need to store the accumulate answer, while the second one must construct a list within the range a and b.
The following code is how to implement a stream, it is just to show that is is not very hard to implement a stream by oneself, since the MIT-scheme has build in stream implementation, the following section, I will use the buildin stream implementation.
The key idea of implementing a stream is to use procedure my-delay to delay the evaluation of an expression, and use my-force to evalute a delayed expression.
#!scheme ;; implement Stream (define (memo-proc proc) (let ((already-run? #f) (result #f)) (lambda () (if (not already-run?) (begin (set! result (proc)) (set! already-run? true) result) result)))) (define (my-delay exp) (memo-proc (lambda () exp))) (define (my-force delayed-object) (delayed-object)) (define the-empty-stream '()) (define (my-stream-null? s) (eq? s the-empty-stream)) (define (my-stream-cons a b) (cons a (my-delay b))) (define (my-stream-car stream) (car stream)) (define (my-stream-cdr stream) (my-force (cdr stream))) (define (my-stream-ref s n) (if (= n 0) (my-stream-car s) (my-stream-ref (my-stream-cdr s) (- n 1)))) (define (my-stream-map proc s) (if (my-stream-null? s) the-empty-stream (my-stream-cons (proc (my-stream-car s)) (my-stream-map proc (my-stream-cdr s))))) (define (my-stream-filter pred stream) (cond ((my-stream-null? stream) the-empty-stream) ((pred (my-stream-car stream)) (my-stream-cons (my-stream-car stream) (my-stream-filter pred (my-stream-cdr stream)))) (else (my-stream-filter pred (my-stream-cdr stream))))) (define (my-stream-for-each proc s) (if (my-stream-null? s) 'done (begin (proc (my-stream-car s) (my-stream-for-each proc (my-stream-cdr s)))))) (define (display-line x) (newline) (display x)) (define (display-stream s) (my-stream-for-each display-line s)) (define test (my-stream-cons 3 (+ 3 3))) ;Value: test (my-stream-car test) ;Value: 3 (my-stream-cdr test) ;Value 6
Section 3.5.2 Infinite Streams
Stream is useful to represent infinite sequence, such as natural number(1,2,3,...) and so on. The following content I will use the MIT-scheme's build-in stream function instead implement by myself like the last section.
Natural number example:
#!scheme (define (from n) (cons-stream n (from (+ n 1)))) (define nats (from 1)) (stream-head nats 10) ;Value 13: (1 2 3 4 5 6 7 8 9 10)
Here is the impressive example of sieve method to get the primes number by using the stream:
#!scheme (define (divisible? x y) (= (remainder x y) 0)) (define (not-divisible? x y) (not (divisible? x y))) (define (sieve stream) (cons-stream (stream-car stream) (sieve (stream-filter (lambda (x) (not-divisible? x (stream-car stream))) (stream-cdr stream))))) (define primes (sieve (from 2))) (stream-head primes 20) ;Value 16: (2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71) (stream-ref primes 100000) ;Aborting!: out of memory ;Aborting!: out of memory ;Aborting!: out of memory C-c C-c? ;Quit!
Because we use stream, it does not calculate the prime unless we need it. But we should also notice that this method is extreamly in using memory when apply to large number and since everytime, it delay the calculation of the tail of the stream, it wrap a new not-divisible? test of the tail everytime we cons the stream. One should take care when apply this to large prime sieve problem.
The following text give a better stream based sieve method:
#!scheme (define primes (cons-stream 2 (stream-filter prime? (from 3)))) (define (prime? n) (define (iter ps) (cond ((> (square (stream-car ps)) n) #t) ((divisible? n (stream-car ps)) #f) (else (iter (stream-cdr ps))))) (iter primes)) (stream-ref primes 100000) ;Value: 1299721
Notice, the sieve procedure use a test function prime? to test the prime, so it does not need to wrap a new function every time we cons a stream, and also do not need to test the divisibility of every number before the stream car, instead only to test the prime number less than the sqrt root of the number. Although the procedure still runs slow, it will not run into out of memory problem.
Exploiting the Stream Paradigm
Stream with delayed evaluation can be a powerful modeling tool, providing many of the benefits of local state and assignment. Moreover, they avoid some of the theoretical tangles that accompany the introduction of assignment into a programming language.
The stream approach can be illuminating because it allows us to build systems with different module boundaries than system organized around assignment to state variables. For example, we can think of an entire time series (or signal) as a focus of interest, rather than the value of the state variables as individual moments. This makes it convenient to combine and compare componenets of state from different moments.
This section explore three type of paradigm of stream, namely: - Formulating iterations as stream processes - Infinite stream of pairs - Stream as signals
Formulating iterations as stream processes
Take the sqrt in chapter 1 as example, using stream, we can build a sqrt procedure as follow:
#!scheme (define (average x y) (/ (+ x y) 2.0)) (define (sqrt-improve guess x) (average guess (/ x guess))) (define (sqrt-stream x) (define guesses (cons-stream 1.0 (stream-map (lambda (guess) (sqrt-improve guess x)) guesses))) guesses) (stream-head (sqrt-stream 2.0) 4) ;Value 13: (1. 1.5 1.4166666666666665 1.4142156862745097)
Or the pi series as an example, defined as: pi / 4 = 1 - 1/3 + 1/5 - 1/7 + ...
#!scheme (define (partial-sum stream) (let ((hh (stream-car stream))) (cons-stream hh (stream-map (lambda (x) (+ x hh)) (partial-sum (stream-cdr stream)))))) (define (scale-stream stream factor) (stream-map (lambda (x) (* x factor)) stream)) (define (pi-summands n) (cons-stream (/ 1.0 n) (stream-map - (pi-summands (+ n 2))))) (define pi-stream (scale-stream (partial-sum (pi-summands 1)) 4)) (stream-head pi-stream 4) ;Value 16: (4. 2.666666666666667 3.466666666666667 2.8952380952380956)
The Swiss mathematician Leonhard Euler(eighteenth-century) give a method to accelerator the converge's speed is more fast than the origin one but converge to the same result. His method work for the series with alternative sign, so the pi example is suitable to illustrate.
If S(n) is the nth term of the origin sum sequence, then the accelerated sequence has terms:
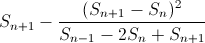
The transform code as follows :
#!scheme (define (euler-transform s) (let ((s0 (stream-ref s 0)) ;S(n-1) (s1 (stream-ref s 1)) ;S(n) (s2 (stream-ref s 2)));S(n+1) (cons-stream (- s2 (/ (square (- s2 s1)) (+ s0 (* -2 s1) s2))) (euler-transform (stream-cdr s))))) (stream-head (euler-transform pi-stream) 4) ;Value 17: (3.166666666666667 3.1333333333333337 3.1452380952380956 3.1396825396825396)
We can see that the converge's speed is much more faster than the naive one. In fact, we can do even better, by accelerating the accelerated sequence. Namely, we can create a stream of stream, wich is called tableau, in which each stream is the transform of the preceding ones:
#!scheme (define (make-tableau transform s) (cons-stream s (make-tableau transform (transform s))))
This code take a transform and a stream, and generate a stream of stream like this:
S(00) S(01) S(02) S(03) S(04) .... S(10) S(11) S(12) S(13) .... S(20) S(21) S(22) .... S(30) S(31) .... ..........
Each line is the transformed stream of the previous line. Then we get the first element of each line to make a sequence, and will get an even faster convergent sequence.
#!scheme (define (accelerated-sequence transform s) (stream-map stream-car (make-tableau transform s))) (stream-head (accelerated-sequence euler-transform pi-stream) 4) ;Value 18: (4. 3.166666666666667 3.142105263157895 3.1415993573190044)
Infinite streams of pairs
In fact, we can view the integer pair as rational number, since we can view integer pair (i, j) as rationa number i/j.And since rational number is countable(see this link), we can say that integer pair is countable.
(0 0) | (0 1) (0 2) (0 3) (0 4) ..... ------------------------------------- | (1 1) (1 2) (1 3) (1 4) ..... | (2 2) (2 3) (2 4) ..... | (3 3) (3 4) ..... | (4 4) .....
We can view it as the picture show aboove, if we take to natural number stream, we can split it into the three part as the picture show, (0 0) as the head of the integer pair stream, then the same line is another stream, and the right bottom side is a similar integer pair stream start from (1 1).
The code to generate all integer pair (i, j) (i <= j) is as follow:
#!scheme (define (from n) (cons-stream n (from (+ n 1)))) (define nats (from 0)) (define (interleave s1 s2) (if (stream-null? s1) s2 (cons-stream (stream-car s1) (interleave s2 (stream-cdr s1))))) (define (pairs s t) (cons-stream (list (stream-car s) (stream-car t)) (interleave (stream-map (lambda (x) (list (stream-car s) x)) (stream-cdr t)) (pairs (stream-cdr s) (stream-cdr t))))) (stream-head (pairs nats nats) 10) ;Value 16: ((0 0) (0 1) (1 1) (0 2) (1 2) (0 3) (2 2) (0 4) (1 3) (0 5))
The procedure interleave is used to alternative select element from two stream.
Updated