Wiki
Clone wikiCAFE / vignette
CAFE Package HowTo
Introduction
So, you have downloaded the CAFE package, and are wondering "What on Earth can I do with this?". In answering this question, we can first of all refer to the package name: I’m sure you’d all have thought about a nice warm cup of coffee, but in reality CAFE stands for Chromosomal Aberrations Finder in Expression data. Now, that might not tell you much, so here is a slightly better - albeit longer - summary of what it does: CAFE analyzes microarray expression data, and tries to find out whether your samples have any gross chromosomal gains or losses. On top of that, it provides some plotting functions - using the ggplot2 package - to give you a nice visual tool to determine where those aberrations are located. How it exactly does this is something you can find later in this document. CAFE does not invent any new algorithms for the detection of chromosomal aberrations. Instead, it takes the approach of Ben-David et al [1], and molds it into an easy-to-use R package.
Prerequisites
As all software packages, CAFE has its requirements. You should
preferably have the latest version of R, but at the very least version
2.10. Other dependencies can be found in the DESCRIPTION file. Some
packages imported by CAFE require you to have libcurl installed in
your system, and by extension the RCurl and Rtracklayer packages. If
these are not yet installed in your system, this could take a while to
install.
Preparing your file system
CAFE analyzes microarray expression data. That means that without anything to analyze, it won’t do anything at all. So, how do we fix this obvious problem? As a starter, CAFE only analyzes .CEL files. This means that CAFE will only work with data from Affymetrix microarrays. Illumina or other platforms unfortunately will not work. To prepare your filesystem correctly, follow the following steps.
Put all CEL files in a folder and then start R in that folder.
Alternatively, you can set the working directory to this folder by
setwd("/some/folder/path/"). And we’re done. It’s that simple. See
figure 1 for a screenshot of how this looks in a file manager.
See figure 1 for a screenshot of how this is layed out
Analysis
Now we’re ready to start analyzing our dataset(s).
CAFE provides the ProcessCels() function. This function takes four
arguments: threshold.over, threshold.under remove_method and
local_file. The threshold will determine which probes are going to be
considered as overexpressed. The default setting is
threshold.over=1.5, meaning that probes with a relative expression
over 1.5 times median will be considered overexpressed. Likewise
threshold.under determines which probesets will be considered
underexpressed. As for the remove_method argument, this determines in
what way ProcessCels will remove duplicate probes. See section 3.1 for
an overview of this option. The ProcessCels() function will basically
suck up all your CEL files in your working directory - but don’t worry,
they’ll still be there in your file system - and perform some number
magic on them; it will normalize, calculate probes that are
overexpressed, log2 transform and remove duplicates. It returns you a
list object of your entire dataset, which the rest of CAFE
requires to function.
So lets try that. First of all, we of course need to load the package:
library(CAFE)
## Loading required package: biovizBase ## Loading required package: GenomicRanges ## Loading required package: BiocGenerics ## Loading required package: parallel ## ## Attaching package: 'BiocGenerics' ## ## The following objects are masked from 'package:parallel': ## ## clusterApply, clusterApplyLB, clusterCall, clusterEvalQ, ## clusterExport, clusterMap, parApply, parCapply, parLapply, ## parLapplyLB, parRapply, parSapply, parSapplyLB ## ## The following object is masked from 'package:stats': ## ## xtabs ## ## The following objects are masked from 'package:base': ## ## anyDuplicated, append, as.data.frame, as.vector, cbind, ## colnames, duplicated, eval, evalq, Filter, Find, get, ## intersect, is.unsorted, lapply, Map, mapply, match, mget, ## order, paste, pmax, pmax.int, pmin, pmin.int, Position, rank, ## rbind, Reduce, rep.int, rownames, sapply, setdiff, sort, ## table, tapply, union, unique, unlist ## ## Loading required package: IRanges ## Loading required package: XVector ## Loading required package: ggbio ## Loading required package: ggplot2 ## Need specific help about ggbio? try mailing ## the maintainer or visit http://tengfei.github.com/ggbio/ ## ## Attaching package: 'ggbio' ## ## The following objects are masked from 'package:ggplot2': ## ## geom_bar, geom_rect, geom_segment, ggsave, stat_bin, ## stat_identity, xlim ## ## ## Attaching package: 'CAFE' ## ## The following objects are masked _by_ '.GlobalEnv': ## ## discontSmooth, slidSmooth
Then, we should set our working directory to the dataset folder if we’re not already there.
setwd("/some/path")
Now we’re there we can process the CEL files.
datalist <- ProcessCels()
A moment of reproducibillity
The stuff we’ve done above here is unfortunately not really
reproducible. It requires you to have .CEL files in a folder called
/some/path in your home directory, and that’s of course not very
pretty. So to keep the rest of this document reproducible, the CAFE
package comes together with a data object. This is the list object
returned by ProcessCels() when processing both
GSE10809
and
GSE6561.
data("CAFE_data") # will put object named CAFE_data in your global environment
Statistics
So now we come to the core of CAFE: finding which chromosomes are significantly over- or underexpressed. CAFE uses thresholding to determine which probes are overexpressed or underexpressed. We use the probes we deemed overexpressed by our threshold to create a contingency table which can then be used in an Exact Fisher or Chi-Square test. Basically we assume that everything over our defined threshold.over is really overexpressed, and everything uder our defined threshold.under is underexpressed.
To calculate p-values for chromosomes, we will use the
chromosomeStats() function. We can then also select which test (fisher
or chi square) we want to use. When performing multiple tests (i.e. if
we are testing multiple chromosomes), we need to correct our p-values
for type I errors. We can therefore set the bonferroni argument to
true when testing multiple chromosomes. The enrichment argument
controls which side (over- or underexpressed) we are testing for.
# we first have to decide which samples we want to use. names(CAFE_data[[2]]) #to see which samples we got
## [1] "GSM151738.CEL" "GSM151739.CEL" "GSM151740.CEL" "GSM151741.CEL" ## [5] "GSM272914.CEL" "GSM272915.CEL" "GSM272916.CEL" "GSM272917.CEL" ## [9] "GSM272918.CEL" "GSM272919.CEL" "GSM272920.CEL" "GSM272921.CEL"
sam <- c(1, 3) #so we use sample numbers 1, and 3 to compare against the rest chromosomeStats(CAFE_data, chromNum = 17, samples = sam, test = "fisher", bonferroni = FALSE, enrichment = "greater") # we are only testing 1 chromosome
## Chr17 ## 3.989e-48
This uses an Exact Fisher test. Technically speaking, this is better than a chi square test, but can be slower for very large sample sizes. We can also do a chi square test, which is slightly faster.
chromosomeStats(CAFE_data, chromNum = 17, samples = sam, test = "chisqr", bonferroni = FALSE, enrichment = "greater")
## Chr17 ## 1.188e-05
As you will have seen, the output of this is different from
test="fisher". The reason for this is that the Fisher test gives an
exact p-value, whereas a chi square test is just an approximation.
But if we now want to test multiple chromosomes, we have to correct our p-values
chromosomeStats(CAFE_data, chromNum = "ALL", samples = sam, test = "fisher", bonferroni = TRUE, enrichment = "greater")
## Chr1 Chr2 Chr3 Chr4 Chr5 Chr6 Chr7 ## 1.000e+00 1.000e+00 1.000e+00 1.021e-01 3.637e-01 1.000e+00 1.000e+00 ## Chr8 Chr9 Chr10 Chr11 Chr12 Chr13 Chr14 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 3.809e-42 3.868e-01 1.000e+00 ## Chr15 Chr16 Chr17 Chr18 Chr19 Chr20 Chr21 ## 1.000e+00 1.000e+00 8.777e-47 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## Chr22 ## 1.000e+00
The results which we got might be all nice and well - there seems be something amiss with chromosome 17 - but preferably we would like to delve a bit deeper. We would like to know which chromosome bands are duplicated or lost. To do this we can use the same syntax as for chromosomes, except that we are using a different function:
bandStats(CAFE_data, chromNum = 17, samples = sam, test = "fisher", bonferroni = TRUE, enrichment = "greater") #multiple bands per chromosome, so need bonferroni!
## 17cen-q12 17p11.1 17p11.2 17p11.2-p12 17p12 ## 1.000e+00 1.000e+00 8.009e-17 1.000e+00 1.000e+00 ## 17p12.3 17p12-p11.2 17p13 17p13.1 17p13.1-p12 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17p13.2 17p13.3 17p13-p12 17pter-p11 17q ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q11 17q11.1 17q11.1-q11.2 17q11.2 17q11.2-q12 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q11-q12 17q11-q21 17q11-q21.3 17q11-qter 17q12 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q12-q21 17q12-q21.1 17q21 17q21.1 17q21.1-q21.3 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q21.2 17q21.3 17q21.31 17q21.32 17q21.33 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q21.3-q22 17q21-q22 17q21-q23 17q21-q24 17q21-qter ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q22 17q22.2 17q22-q23 17q22-q23.2 17q23 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q23.1 17q23.2 17q23.2-q25.3 17q23.3 17q23-q24 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q24 17q24.1 17q24.2 17q24.3 17q24-q25 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17q25 17q25.1 17q25.2 17q25.2-q25.3 17q25.3 ## 1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00 ## 17qter ## 1.000e+00
So this way we see that there is most likely a duplication around band 17p11.2
Plotting
So now we know that chromosome 17 for these two samples is aberrant, but
we would like to plot that. A picture says more than a thousand words -
as the saying goes. CAFE provides four functions for plotting
samples, rawPlot(), slidPlot(), discontPlot() and facetPlot().
Raw plots
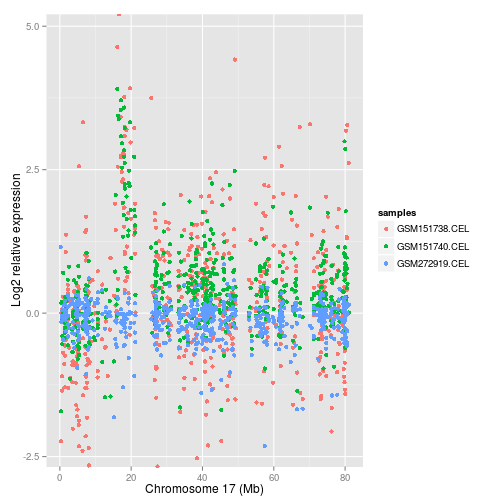
The rawPlot() function plots each individual probe along the
chromosome with its ’raw’, unaltered, log2 relative expression value.
This can give a very rough overview of what is happening. As a visual
tool, an ideogram of the chromosome can be plotted over the plot. See
figure 2 for an example.
rawPlot(CAFE_data, samples = c(1, 3, 10), chromNum = 17)
## Writing plot to Chr17Mul
Sliding plots
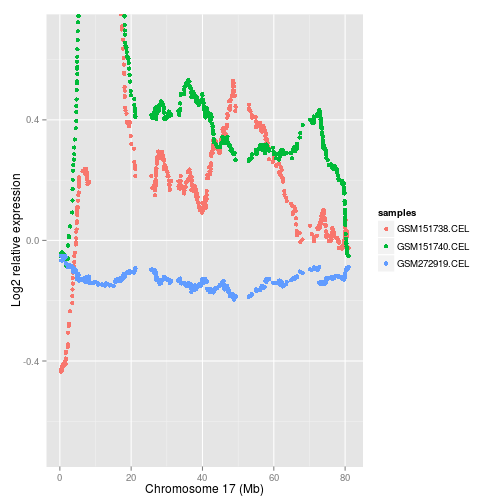
The plots given by rawPlot() are often not very informative since the
within-sample variation in expression levels is quite high. The
slidPlot() function solves this problem by applying a sliding average
to the entire sample. As such, patterns become visible that would
otherwise have went unnoticed. The function has two extra arguments as
rawPlot(): if combine=TRUE a raw plot will be plotted in the
background. The size of the sliding window can be determined by argument
k. See figure 3 for an example.
slidPlot(CAFE_data, samples = c(1, 3, 10), chromNum = 17, k = 100)
## Writing plot to Chr17slidMul
Discontinuous plots
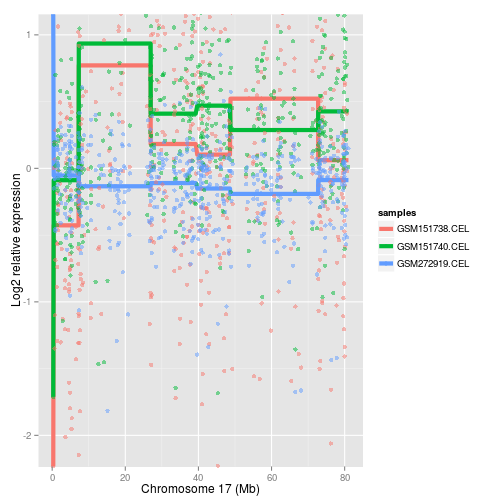
In reality, there can only be an integer number of copy numbers for a
given region (be it an entire chromosome or a band). One cannot 2.5
times duplicate a region; no, it is 0, 1, 2, 3 times etc. Also, there
should be a defined boundary where the duplication or loss begins and
ends. Yet, functions like slidPlot() will give smooth transitions and
variable regions, which is a relatively poor reflection of what is
actually happening. As such, we need a discontinuous smoother rather
than a sliding average smoother. A discontinuous smoother is a smoother
which produces distinct "jumps" rather than smooth transitions. The
discontPlot() function implements such a discontinuous smoother -
called a Potts filter. The smoothness (i.e. amount of jumps) can be
determined by setting parameter gamma. A higher gamma will result in a
smoother graph, with less jumps. See figure 4 for an example.
discontPlot(CAFE_data, samples = c(1, 3, 10), chromNum = 17, gamma = 100)
## Writing plot to Chr17discMul
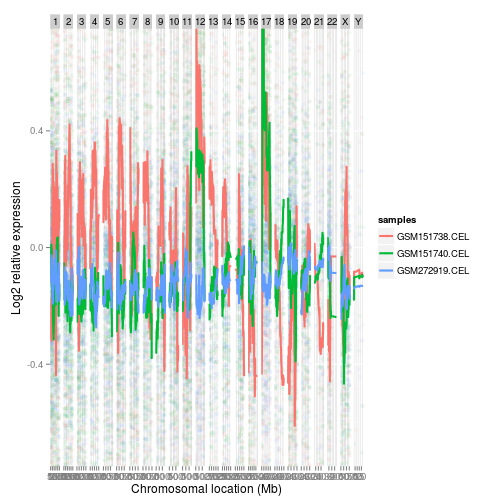
Facet plots
With the facetPlot() function you can plot all chromosomes stitched
together horizontally in one single splot. It includes options to use
either a sliding average smoother. See figure 4 for an example..
facetPlot(CAFE_data, samples = c(1, 3, 10), slid = TRUE, combine = TRUE, k = 100)
## Writing plot to FacetSlidMul
In a nutshell
As follows from the above, CAFE analysis basically boils down to just three steps
-
data <- ProcessCels() -
xxxStats(data, ...) -
xxxPlot(data, ...)
For instance:
data <- ProcessCels() chromosomeStats(data, samples = c(1, 3), chromNum = "ALL") discontPlot(data, samples = c(1, 3), chromNum = "ALL", gamma = 100)
Behind the scenes
Normalization
Affymetrix CEL files are read in and normalized by the justRMA()
function in the affy package. Absent probes are then found (by the
mas5calls function), and are subsequently removed if absent in more
than 20% of samples. After normalization is complete, relative
expression values (to median) are calculated. The remove_method
argument controls which duplicate probes are removed from the dataset.
When remove_method=0, no duplicate probes will be removed. When
remove_method=1, duplicate probes linking to the same gene will be
removed such that each gene only links to one single probe, according to
the following priorities:
-
Probes with
..._atare preferably retained -
Probes with
...a_at -
Probes with
...n_at -
Probes with
...s_at -
And finally probes with
...x_at
When this still results in multiple probes per gene, the probe with the
earliest chromosomal location is retained. When remove_method=2,
duplicate probes are only removed when they link to the exact same
location, using the same priority list as specified above.
Category testing
When using chromosomeStats() and bandStats() the dataset is
eventually split into four categories:
-
Whole dataset & On Chromosome (or band)
-
Whole dataset & Overexpressed & On Chromosome (or band)
-
Sample(s) & On Chromosome (or band)
-
Sample(s) & Overexpressed & On Chromosome (or band)
The number of probes for each category are counted, and saved in a so-called contingency table. Then we test the likelihood that Sample(s) occurs within Whole via either the Exact Fisher test or the Chi Square test. The Exact Fisher test supplies exact p-values, whereas the Chi Square test supplies merely an approximation. However, the Exact Fisher test can be slower than a Chi Square test, and the Chi Square test increases in accuracy with increasing sample size.
"Overexpressed" is defined as those probes which were over the set
threshold - the threshold.over argument in ProcessCels(). Likewise,
"underexpressed" is defined as those probes which were under the set
threshold - argument threshold.under. Please note that these
thresholds are a defined as a fraction of median expression value for
each probe.
Smoothers
Sliding average
With the moving average we attempt to the smooth the raw data so that
patterns emerge. We have a set of points 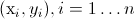 ,
which is ordered such that
,
which is ordered such that 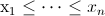 . Since we plotting
chromosomal location versus log2 relative expression,
. Since we plotting
chromosomal location versus log2 relative expression, 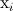 refers to
chromosomal locations and
refers to
chromosomal locations and 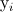 refers to log2 relative expressions.
Since chromosomal locations are integers,
refers to log2 relative expressions.
Since chromosomal locations are integers,
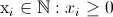 , and since log2 relative expressions can
be any real number
, and since log2 relative expressions can
be any real number 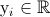 . We have a sliding average
windows, denoted
. We have a sliding average
windows, denoted 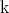 , which determines the smoothness. We are
reconstructiong
, which determines the smoothness. We are
reconstructiong 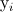 (the log2 relative expressions) to come to a
smoother
(the log2 relative expressions) to come to a
smoother 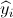 . For
. For 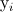 at least
at least 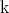 -elements from the boundary,
the smoother is calculated as in equation 1. For the remaining
-elements from the boundary,
the smoother is calculated as in equation 1. For the remaining
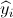 , where
, where 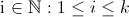 and
and 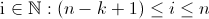 , we first define two variables
, we first define two variables
 and
and 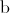 , where
, where 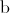 and
and 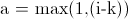 . The
remaining
. The
remaining 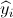 are then calculated using equation 2.
are then calculated using equation 2.
Equation 1: 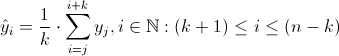
Equation 2: 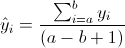
Discontinuous smoother
The discontinuous smoother used in discontPlot(), is essentially a
minimization problem. We again have a set of points
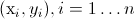 . This set is ordered in such manner that
. This set is ordered in such manner that
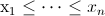 . For our particular problem
. For our particular problem 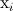 refers to
chromosomal coordinates, such that
refers to
chromosomal coordinates, such that 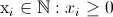 .
Conversely,
.
Conversely, 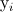 refers to log2 relative expressions, such that
refers to log2 relative expressions, such that
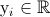 . We want to reconstruct
. We want to reconstruct 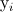 in such a way that
the reconstruction - called
in such a way that
the reconstruction - called 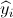 - closely resembles
- closely resembles 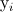 but
has as little jumps as possible. A jump is defined as
but
has as little jumps as possible. A jump is defined as
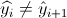 . The reconstruction
. The reconstruction 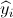 can be
constructed by minimizing the following function:
can be
constructed by minimizing the following function:
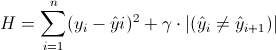
In the above formula, || denotes cardinality. The first term in the
formula denotes a least squares goodness-of-fit term. The second term
determines how strict the formula is. A higher 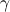 will result in a
flatter result, with fewer jumps, and this
will result in a
flatter result, with fewer jumps, and this 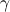 can be any number
over 0. The entire formula is called a Potts filter. The mathematics
behind this formula is described in detail by Winkler et al [2].
can be any number
over 0. The entire formula is called a Potts filter. The mathematics
behind this formula is described in detail by Winkler et al [2].
The implementation in discontPlot() uses the algorithm descibed by
Friedrich et al [3].
Non-Affymetrix data
Even though CAFE is designed to work only with Affymetrix .CEl
files, it is possible to analyse non-affymetrix data via a workaround.
For CAFE to work with non-affymetrix data, it is necessary you
provide the correct data structure which we use to analyse our data. The
major structure the software works with is a list of lists
structure. The list contains three lists - named $whole, $over
and $under - which both contain data frames for each and every sample
using the following format:
-
$ID, some identifier (probe IDs in affymetrix) (character vector) -
$Sym, gene symbol (character vector) -
$Value, log2 transformed expression value (numerical vector) -
$LogRel, log2 transformed relative expressions (as a function of mean) (numerical vector) -
$Loc, chromosomal locations in bp (integer vector) -
$Chr, chromosome number (character vector) -
$Band, cytoband (character vector)
For instance
str(CAFE_data$whole[[1]])
## 'data.frame': 10442 obs. of 8 variables: ## $ ID : chr "1053_at" "121_at" "1316_at" "1487_at" ... ## $ Sym : chr "RFC2" "PAX8" "THRA" "ESRRA" ... ## $ Value : num 6.48 6.72 4.17 6.39 7.41 ... ## $ LogRel: num -2.077 -0.336 -0.435 -0.814 -1.672 ... ## $ Loc : int 73646002 113974938 38219184 64073043 43562239 26722694 90039000 196439228 27941782 34175215 ... ## $ Chr : chr "7" "2" "17" "11" ... ## $ Band : chr "7q11.23" "2q13" "17q11.2" "11q13" ... ## $ Arm : chr "7q" "2q" "17q" "11q" ... ## - attr(*, "na.action")=Class 'omit' Named int [1:95] 44 53 54 55 56 57 187 194 206 220 ... ## .. ..- attr(*, "names")= chr [1:95] "44" "53" "54" "55" ...
The $whole list should contain data for all probes, the $over list should only contain those probes which are deemed overexpressed (not required if one uses thresholding=FALSE). The order of probes and locations in $whole should be identical across all samples. Each list element (i.e. the dataframes) is named according to its sample name.
For instance
print(names(CAFE_data$whole))
## [1] "GSM151738.CEL" "GSM151739.CEL" "GSM151740.CEL" "GSM151741.CEL" ## [5] "GSM272914.CEL" "GSM272915.CEL" "GSM272916.CEL" "GSM272917.CEL" ## [9] "GSM272918.CEL" "GSM272919.CEL" "GSM272920.CEL" "GSM272921.CEL"
References
[1]: Uri Ben-David, Yoav Mayshar, and Nissim Benvenisty. Virtual karyotyping of pluripotent stem cells on the basis of their global gene expression profiles. Nature protocols, 8(5):989–997, 2013. http://dx.doi.org/10.1038/nprot.2013.051
[2]: G Winkler, Volkmar Liebscher, and V Aurich. Smoothers for Discontinuous Signals. Journal of Nonparametric Statistics, 14:203–222, 2002. http://dx.doi.org/10.1080/10485250211388
[3]: F Friedrich, a Kempe, V Liebscher, and G Winkler. Complexity Penalized M- Estimation. Journal of Computational and Graphical Statistics, 17(1):201– 224, March 2008. http://dx.doi.org/10.1198/106186008X285591
Updated