Testing the accuracy of 2D interpolation within CosmoSIS

The purpose of the exercise described here is to test how the number of points in a linear matter power spectrum P(k) affects the accuracy to which we can interpolate it. The CosmoSIS module pktest was created for this purpose. A summary of the testing process and its results follow.

The testing process:
The methodology of pktest is summarised in Fig 1. The input is a z=0 power spectrum generated by an upstream module. Here we used CAMB, but other code (eg. crl_eisenstein_hu) would serve equally well. The number of k-modes in the input spectrum is controlled by a user-defined parameter, which instructs CAMB to insert additional modes, evenly spaced in log space, between each pre-existing pair.

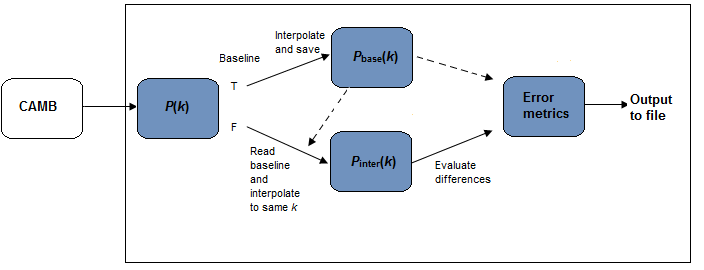
Fig 1. Flow diagram showing the testing pipeline. The solid arrows denote calculations performed by pktest. The dashed lines represent data read in from a file outside the pipeline.

The basic process is as follows:

1. Read in a very high resolution baseline spectrum, interpolate and save. This is taken as a good approximation for the smooth function P(k) that CAMB samples.
2. For subsequent calls, read in a lower resolution spectrum and interpolate out to the baseline points.
3. Compare the interpolated and baseline spectra on a point-by-point basis. Differences can then be used as measures of the error introduced by interpolation.

By calling the pipeline recursively, we can plot these measures as functions of the number of points available for interpolation.

Results:
Three accuracy measures are shown in the plots (Fig 2-4) below. The first shows the maximum single-point fractional difference between the spectra (maxdiff). This is included as a gauge of worst-case deviation. It is useful as an upper limit interpolation uncertainty in calculations involving single points. The second is the mean deviation across all k, cast as an absolute value (meandiff). The last is the difference in the σ8 obtained from the spectra (sig8diff). The latter two are more realistic error estimators for calculations involving integration over an interpolated spectrum. 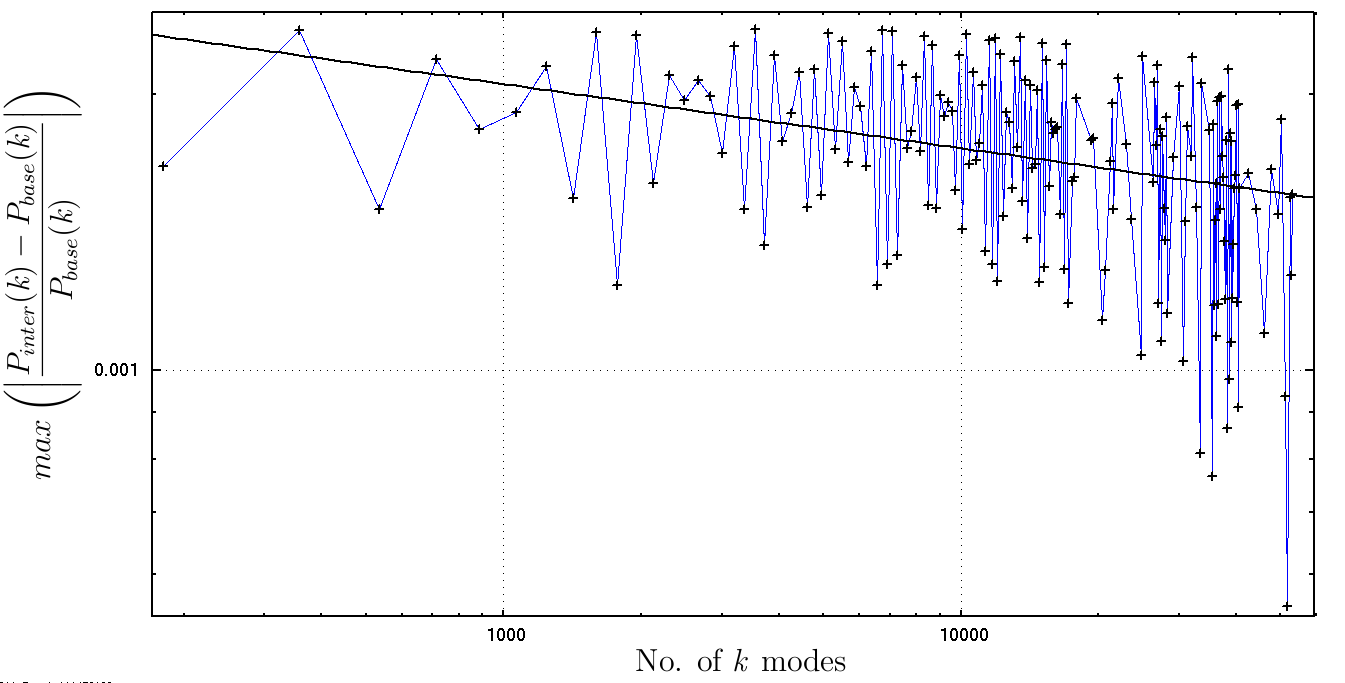Fig 2. Maximum single-point difference between baseline and interpolated P(k). Note that the scatter is thought to be a result of the relative shift in the input and interpolated points as the no. of modes increases.

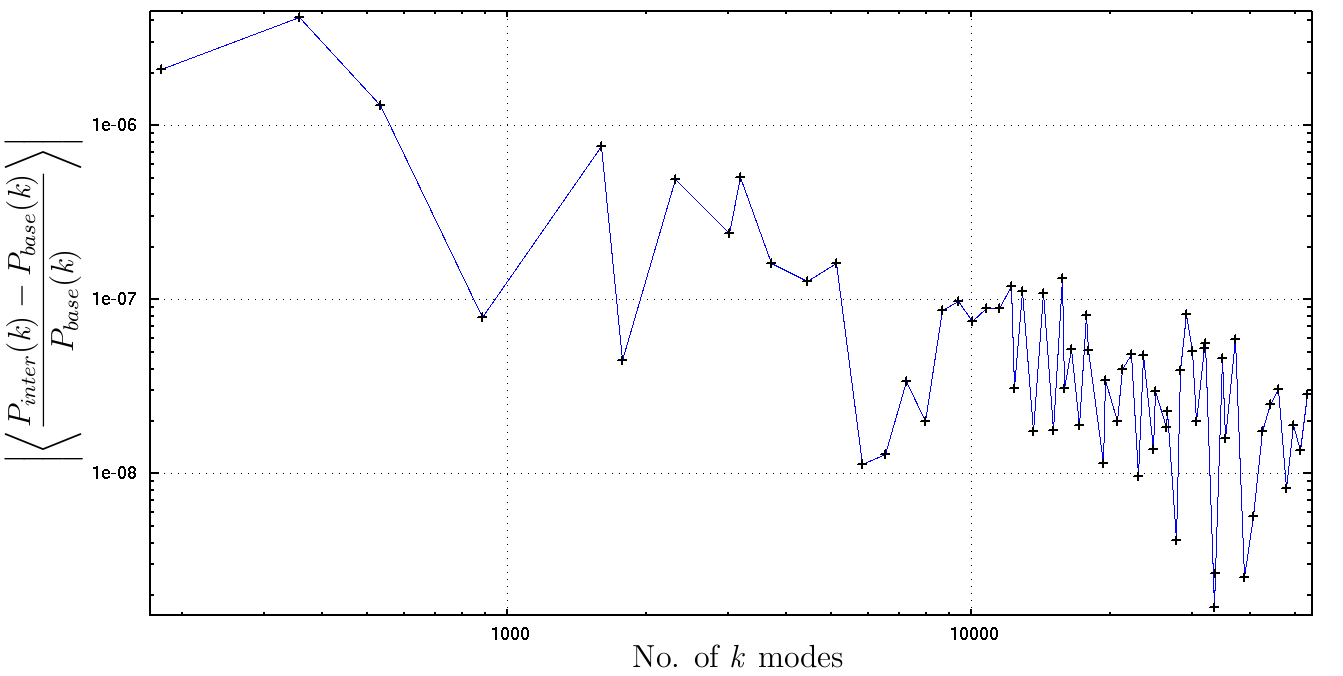Fig 3. Mean fractional difference between baseline and interpolated P(k).

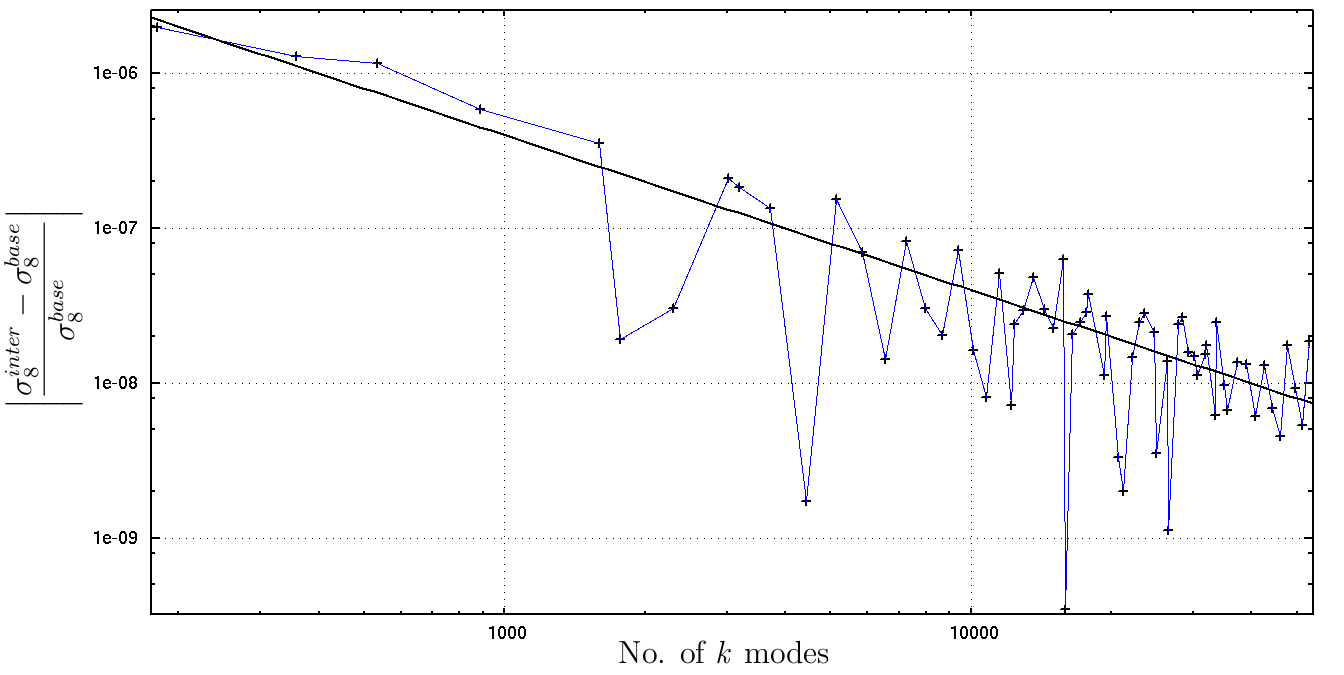Fig 4. Fractional difference in σ8 obtained from baseline and interpolated P(k).

The interpolation errors are clearly very small. The headline result here is that sig8diff and meandiff are ~10^-4% for the default 180-point CAMB spectrum. An order of magnitude improvement in accuracy requires a change in the number of input points by approximately the same factor. The more conservative estimator, maxdiff, is more stable at ~0.2%.

For more information contact Simon Samuroff at sw.samuroff@yahoo.co.uk