###Computational homogenisation###

Keywords: Computational homogenisation, Linear elasticity, High-Order Approximation, Textile composites, Represtative volume element

Problem description

Implementation of the representative volume element (RVE) boundary conditions (including linear displacement, traction and periodic) in a generalized manner using the procedure given in [1] for the textile composite. The homogenised or effective stiffness matrix is calculated, which gives the relation between macro-strain and macro-stress.

Theoretical background

Detailed theoretical background and implementation of the RVE boundary condition, while using hierarchic finite element [2] can be found in the attached pdf file and can be downloaded from Theory and implementation manual

Validation

Before applying the RVE boundary conditions to the actual textile composites RVE, its implementation and validated using a simple linear-elastic cube of unit dimensions. The material properties used in this case are Young’s modulus of E = 200 and Poisson's ratio nu = 0.3. A sample mesh and corresponding x-displacement contours after applying a macro-strain of [1.0, 0.0, 0.0, 0.0, 0.0, 0.0] are shown in Figure 1 (a) and Figure 1 (b) respectively. The final homogenised stiffness matrices calculated using all the three types of boundary conditions, including linear displacement, traction and periodic are shown in Table 1. The homogenized stiffness matrices for the three type of boundary conditions are also compared with one calculated directly from the Hooke's law, which is also given in Table 1. It is clear from Table 1 that as expected, homogenised stiffness matrix calculated for a homogeneous material is the same for all three types of boundary conditions and is also the same as calculated directly from the Hooke's law. In the following, the code is used for a more complex case, i.e. a textile composite RVE.

Figure 1. Mesh and x-contours of displacement for a linear-elastic homogeneous cube

Table 1. Homogenised stiffness matrices for linear-elastic homogeneous cube

Geometry used

A sample geometry of the textile RVE used here is also used in [3], which consists of fibres and matrix part. Elliptical cross sections and cubic splines are used to model the cross-sections and paths of the fibre. Different parameters defining the RVE geometry are given in Figure 2.

Figure 2. Textile composite RVE geometry

Input files

The CUBIT journal file required to generate the input model can be downloaded from here (same file is used for all type of boundary conditions including linear displacement, traction and periodic):

• RVE.jou (CUBIT journal)

The files are also located under /mofem_install/mofem/benchmarks/three_point_bending_graphite_simple_notch_symmetric/ in the MoFEM source and build directories.

Material models

A transversely isotropic material was used for the fibres while an isotropic material was used for the matrix part.

Material properties

Matrix

• Young’s modulus = 3.5 GPa

• Poisson's ratio = 0.35

Fibres

• Young’s modulus in transverse direction E_p = 35 GPa

• Poisson's ratio in transverse direction v_p = 0.26

• Young’s modulus in fibre direction E_z = 70 GPa

• Poisson's ratio in fibre direction v_pz = 0.26

• shear modulus in the fibre direction G_pz = 17.5 GPa

Finite Element Model

The finite element model consists of a 4-node tetrahedral elements as shown in Figure 3. Periodic mesh is created for the RVE, e.g. for every nodes on the positive x-face there is a node on the negative x-face with same y and z coordinates.

Figure 3. Sampel RVE geometry and corresponding mesh

Analysis procedure

First run the potential flow problem to calculate the fibre directions using:

mpirun -np 1 ./potential_flow_all -my_file RVE.cub -ksp_type fgmres -ksp_gmres_restart 1000 -pc_type asm -sub_pc_type lu -ksp_monitor -my_order 1

To run the RVE analysis using linear displacement boundary conditions use:

mpirun -np 1 ./RVE_disp -my_file solution1.h5m -ksp_type fgmres -pc_type lu -pc_factor_mat_solver_package superlu_dist -ksp_monitor -my_order 1 -myapplied_strain 1.0,0.0,0.0,0.0,0.0,0.0 

To run the RVE analysis using traction boundary conditions use:

mpirun -np 1 ./RVE_trac -my_file solution1.h5m -ksp_type fgmres -pc_type lu -pc_factor_mat_solver_package superlu_dist -ksp_monitor -my_order 1 -myapplied_strain 1.0,0.0,0.0,0.0,0.0,0.0 

To run the RVE analysis using periodic boundary conditions use:

mpirun -np 1 ./RVE_periodic -my_file solution1.h5m -ksp_type fgmres -pc_type lu -pc_factor_mat_solver_package superlu_dist -ksp_monitor -my_order 1 -myapplied_strain 1.0,0.0,0.0,0.0,0.0,0.0 

where

myapplied_strain 1.0,0.0,0.0,0.0,0.0,0.0 is an applied macro-strain as [Sig_xx, Sig_yy, Sig_zz, Sig_xy, Sig_xz, Sig_zy]

Results

The potential flow problem is solved independent of the main RVE analysis. Potential flow field and fibres direction are calculated from the potential flow problem, which are then used as input for the main RVE analysis. The potential field and calculated fibres directions are shown in Figure 4.

Figure 4. Potential field (left) and calculated fibres directions (right)

Finally, the full homogenised stiffness matrices with size of (6x6) is calculated for all the three types of boundary conditions for 1st and 2nd order of approximation and is given in Table 2. To calculate the first column of stiffness matrix a macro-strain of [1.0, 0.0, 0.0, 0.0, 0.0, 0.0] is applied to the RVE and homogenised stress is calculated, which is the first column of homogenised stiffness matrix given in columns under strain_xx=1 in Table 1. The controus of x-componenet of the displacement over the RVE due to macro-strain of [1.0, 0.0, 0.0, 0.0, 0.0, 0.0] is given in Figure 5. The homogenised stiffness matrices shown in Table 2 is obtained while using 1st, 2nd and 3rd order approximation, but the developed code can be used for arbitrary order of approximation. Comparison of C11, C22, C33, C12, C13 and C23 for displacement, traction and periodic boundary conditions are shown in Figure 6. It is clear from Table 2 and Figure 6, that response for the periodic boundary conditions case lies between the response of displacement and traction boundary conditions cases, which is coincides with lietrature.

Table 2. Homogenised stiffness matrix with approximation order 1st (left) and 2nd (right)

Figure 5. Contours of x-displacement over the RVE for input macro-strain of [1.0, 0.0, 0.0, 0.0, 0.0, 0.0]

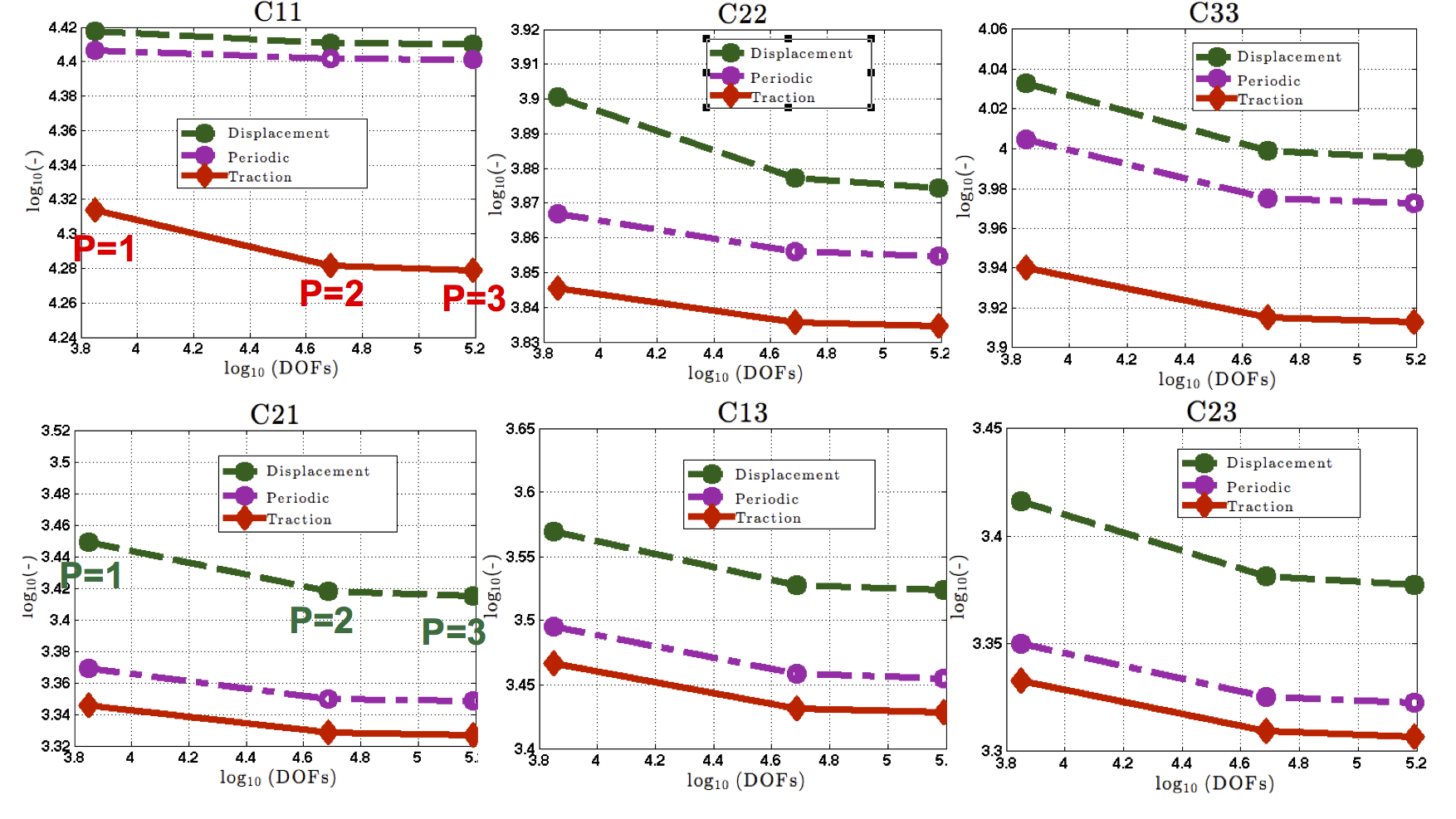
Figure 6. Comparison of C11, C22, C33, C12, C13 and C23 for displacement, traction and periodic boundary conditions

Acknowledgements

Results were obtained as part of the Providing Confidence in Durable Composites (DURACOMP) project sponsored by UK Engineering and Physical Sciences Research Council (EPSRC) (Grant Ref.: EP/K026925/1).

References

1. L. Kaczmarczyk, C. J. Pearce, and N. Bicanic. Scale transition and enforcement of RVE boundary conditions in second-order computational homogenization. International Journal for Numerical Methods in Engineering, 74(3):506–522, 2008.

2. M. Ainsworth and J. Coyle. Hierarchic finite element bases on unstructured tetrahedral meshes. International Journal for Numerical Methods in Engineering, 58(14):2103– 2130, 2003.

3. T. W. Chua. Multi–scale modeling of textile composites. Master’s thesis, Department of Mechanical Engineering, Technische Universiteit Eindhoven, January 2011.

• Created by Zahur Ullah
• any difficulties or suggestions email cmatgu@googlegroups.com