Wiki

Demo 17: Run a Fisher matrix analysis of Dark Energy Survey 2-point data.

Fisher matrices characterize the curvature of a likelihood at its peak, are usually used in cosmology as approximations to a full MCMC analysis - they are much faster, requiring only a handful of evaluations, but cannot capture the full shape of a distribution unless it is very close to purely Gaussian. They are therefore often used for forecasting where approximate constraints suffice. See Wolz et al for a discussion.

The Dark Energy Survey Science Verification likelihood shown here is a weak lensing two-point data set based on very preliminary DES-SV data.

In this demo we will use a Fisher matrix to approximate the likelihood surface of a simplified form of the DES-SV analysis.

Running

Run demo 17 with this command:

cosmosis demos/demo17.ini

It shouldn't take long, but if you are impatient you can run this in parallel. Fisher matrices parallelize very well, and you can use up to 4*n_param processors if you have them. For example:

mpirun -n 4 cosmosis --mpi demos/demo17.ini

The output will be demo17.txt, which will contain the Fisher matrix.

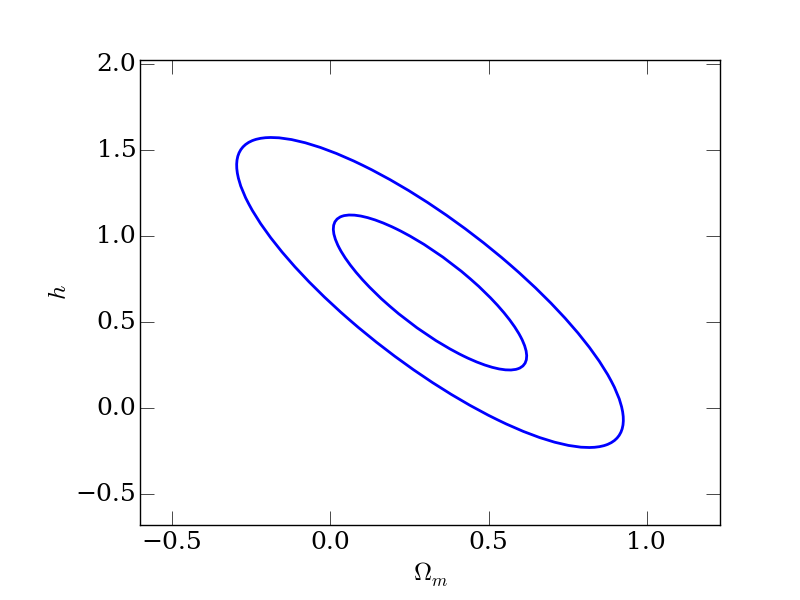
You can plot the ellipses that approximate the likelihood using:

postprocess output/demo17.txt -o plots -p demo17

which will generate, for example, the verbosely named file plots/demo17_2D_cosmological_parameters--sigma8_input_cosmological_parameters--omega_m.png which should look something like this:

2D_cosmological_parameters--omega_m_cosmological_parameters--h0.png

Understanding

Fisher matrices in general

The Fisher matrix is defined as the expectation of the product of the derivatives of the log of the likelihood with respect to pairs of parameters, with each pair filling in a matrix element:

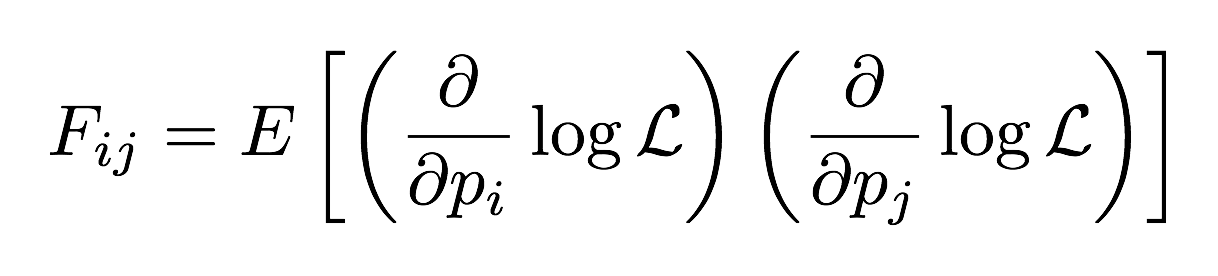
This is usefully evaluated at the peak of the likelihood distribution; we usually only know this perfectly in simulations.

Often the likelihood is a Gaussian with respect to some set of predicted observables v, which are themselves predicted from the input parameters. In this case the Fisher matrix simplifies to:

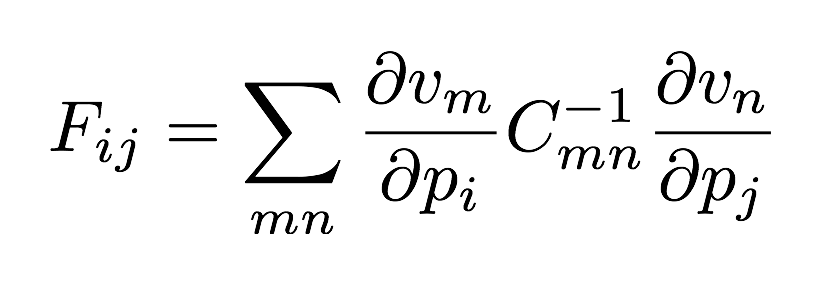
$latex-image-1.png$

This is the form we use here. If we assume the final parameter likelihood is also a Gaussian (which is only an approximation, and does not follow from the data likelihood being a Gaussian unless the observables are linear in the parameters) then the parameter Covariance matrix is the inverse of the Fisher matrix, and we can use this to make a plot of the likelihood given that we also know the peak position.

Fisher matrices are mostly used for forecasting, since then their inaccuracies matter less and the likelihood peak is known exactly.

BEWARE: Fisher matrices can be very unreliable at high dimension!

Fisher Matrices in CosmoSIS

Most of the samplers in CosmoSIS only need the single likelihood number out of the pipeline. The Fisher sampler is different. It needs a whole vector of observables whose derivative it will calculate.

The likelihood modules that go into a Fisher sampler therefore need to supply more information than just the single likelihood numbers - they also need to provide the vector of observables, and inverse data covariance matrix (which is usually just a fixed value).

If your likelihood is a Gaussian then you can take care of all of this by writing it in python and using the CosmoSIS GaussianLikelihood facility.

If you can't or don't want to use that feature, then the pipeline used with the Fisher Matrix sampler needs to save these values to the datablock:

In a section called data_vector
A real 1D vector: name_theory
A real 2D matrix: name_inverse_covariance

where "name" is your choice of name for the variable; the option "likelihoods" in the "[pipeline]" section
is used to choose which data sets to extract.